Chapter: Operations Research: An Introduction : The Simplex Method and Sensitivity Analysis
Algebraic Sensitivity Analysis-Changes in the Right-Hand Side
Algebraic Sensitivity Analysis-Changes
in the Right-Hand Side
In Previous Section , we used the graphical solution to determine the dual prices (the unit worths of
resources) and their feasibility ranges. This section extends the analysis to
the general LP model. A numeric example (the TOYCO model) will be used to
facilitate the presentation.
Example 3.6-2
(TOYCO Model)
TOYCO
assembles three types of toys-trains, trucks, and cars-using three operations.
The daily limits on the available times for the three operations are 430,460,
and 420 minutes, respectively, and the revenues per unit of toy train, truck,
and car are $3, $2, and $5, respectively. The as-sembly times per train at the
three operations are 1, 3, and 1 minutes, respectively. The corresponding times
per train and per car are (2,0,4) and (1,2,0) minutes (a zero time indicates
that the operation is not used).
Letting x1,
x2, and x3 represent the daily number of
units assembled of trains, trucks, and cars, respectively, the associated LP
model is given as:

The
solution recommends manufacturing 100 trucks and 230 cars but no trains. The
associated revenue is $1350.
Determination of Dual Prices. The
constraints of the model after adding the slack variables x4,
x5, and x6 can be written as follows:
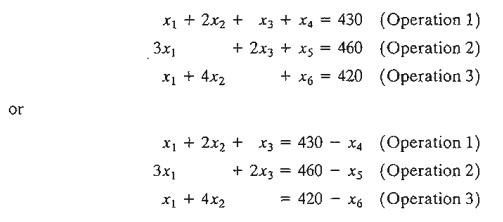
With this
representation, the slack variables have the same units (minutes) as the operation
times. Thus, we can say that a one-minute decrease
in the slack variable is equivalent to a one-minute increase in the operation time.
We can
use the information above to determine the dual
prices from the z-equa-tion in the optimal tableau:
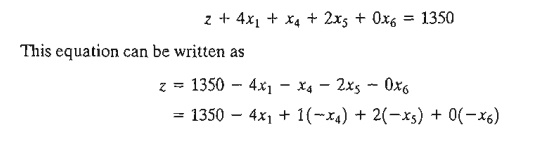
Given
that a decrease in the value of a
slack variable is equivalent to an increase
in its operation time, we get
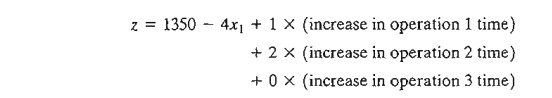
This
equation reveals that (1) a one-minute increase in operation 1 time increases z by $1, (2) a one-minute increase in
operation 2 time increases z by $2,
and (3) a one-minute increase in operation 3 time does not change z.
To
summarize, the z-row in the optimal
tableau:
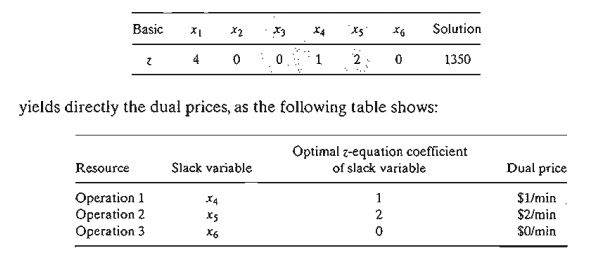
The zero
dual price for operation 3 means that there is no economic advantage in
allocating more production time to this operation. The result makes sense
because the resource is already abundant, as is evident by the fact that the
slack variable associated with Operation 3 is positive (= 20) in the optimum
solution. As for each of Operations 1 and 2, a one minute increase will improve
revenue by $1 and $2, respectively. The dual prices also indicate that, when
allocating additional resources, Operation 2 may be given higher priority
because its dual price is twice as much as that of Operation 1.
The
computations above show how the dual prices are determined from the optimal
tableau for ≤
constraints. For ≥
constraints, the same idea remains applicable except that the dual price will
assume the opposite sign of that associated with the ≤ constraint. As for the case
where the constraint is an equation, the determination of the dual price from
the optimal simplex tableau requires somewhat "involved"
calcula-tions as will be shown in Chapter 4.
Determination of the Feasibility Ranges. Having
determined the dual prices, we show next how the feasibility ranges in which they remain valid are determined. Let DI , Dz, and D3
be the changes (positive or negative) in the daily manufacturing time allocated
to operations 1,2, and 3, respectively. The model can be written as follows:
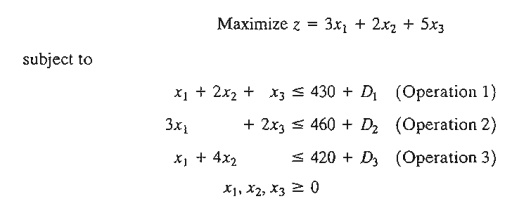
We will
consider the general case of making the changes simultaneously. The special
cases of making change one at a time are derived from these results.
The
procedure is based on recomputing the optimum simplex tableau with the modified
right-hand side and then deriving the conditions that will keep the solution
feasible-that is, the right-hand side of the optimum tableau remains nonnegative.
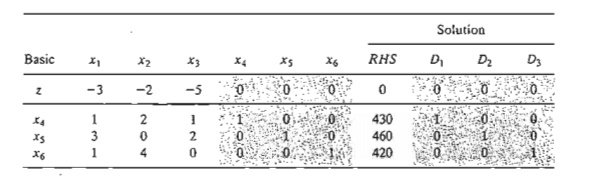
To show how the right-hand side is recomputed, we start by modifying the Solution column of the starting tableau
using the new right-hand sides: 430 + D1
460 + D2, and 420 + D3 . The starting tableau will thus appear
as
The
columns under D1 D2 and D3 are
identical to those under the starting basic columns x4,x5, and x6. This means that when we carry
out the same simplex iterations as in
the original model, the columns in
the two groups must come out identical as well. Effectively, the new optimal
tableau will become
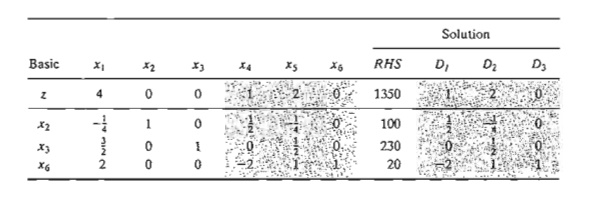
The new
optimum tableau provides the following optimal solution:

Interestingly,
as shown earlier, the new z-value confirms that the dual prices for operations
1,2, and 3 are 1,2, and 0, respectively.
The
current solution remains feasible so long as all the variables are nonnegative,
which leads to the following feasibility
conditions:
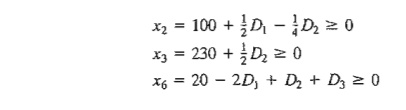
Any
simultaneous changes D1, D2, and D3 that satisfy
these inequalities will keep the solution feasible. If all the conditions are
satisfied, then the new optimum solution can be found through direct
substitution of D1,D2 and D3
in the equations given above.
To
illustrate the use of these conditions, suppose that the manufacturing time
available for operations 1,2, and 3 are 480,440, and 410 minutes respectively.
Then, Dl = 480 - 430 = 50, D2 = 440 - 460 = -20, and D3 = 410 -
420 = -10. Substituting in the
feasibility conditions, we get
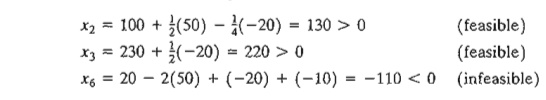
The calculations
show that x6 < 0, hence
the current solution does not remain feasible. Additional calculations will be
needed to find the new solution. These calculations are discussed in Chapter 4
as part of the post-optimal analysis.
Alternatively,
if the changes in the resources are such that D1 = -30, D2 = -12, and D3 = 10, then
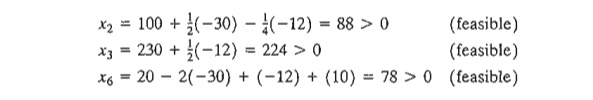
The new
feasible solution is x1 = 88, x3 = 224, and
x6 = 68
with z = 3(0) + 2(88) +
5(224) = $1296. Notice that the optimum
objective value can also be computed as z = 1350 + 1( -30) + 2( -12) = $1296.
The given
conditions can be specialized to produce the individual feasibility ranges that result from changing the resources one at a time (as defined in Section
3.6.1).
Case 1. Change in operation 1 time
from 460 to 460 + D1 minutes. This
change is equiv-alen to setting D2 = D3 = 0 in the simultaneous
conditions, which yields
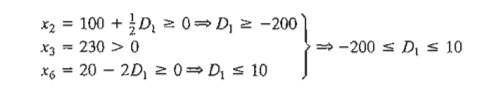
Case 2. Change in operation 2 time
from 430 to 430 + D2 minutes. This change is equivalent to setting D1 = D3 = 0 in
the simultaneous conditions, which yields
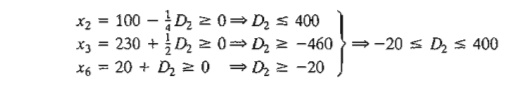
Case 3. Change in operation 3 time
from 420 to 420 +
D3 minutes. This
change is equivalent to setting D1 = D2
= 0 in the simultaneous conditions, which yields
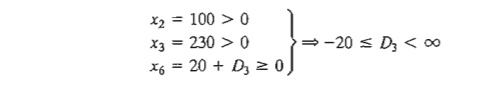
We can
now summarize the dual prices and their feasibility ranges for the TOYCO model
as follows:

It is
important to notice that the dual prices will remain applicable for any simultaneous changes that keep the
solution feasible, even if the
changes violate the indi-vidual ranges. For example, the changes D1 = 30, D2 = -12, and D3
= 100, will keep the solution feasible even though D1 = 30
violates the feasibility range -200 ≤ Dl ≤ 10, as
the following computations show:
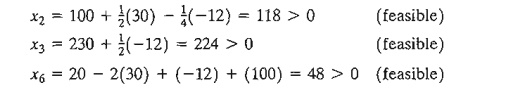
This
means that the dual prices will remain applicable, and we can compute the new
optimum objective value from the dual prices as z = 1350 + 1(30) + 2( -12) + 0(100) = $1356
The
results above can be summarized as follows:
1. The
dual prices remain valid so long as the changes Di , i = 1,2, ... , m, in the
right-hand sides of the constraints satisfy all the feasibility conditions when
the changes are simultaneous or fall within the feasibility ranges when the
changes are made individually.
2. For
other situations where the dual prices are not valid because the simultaneous
feasibility conditions are not satisfied or because the individual feasibility
ranges are violated, the recourse is to either re-solve the problem with the
new values of Di or apply the post-optimal analysis
presented in Chapter 4.
PROBLEM SET 3.6et
1. In the
TOYCO model, suppose that the changes DI , Dz, and D3
are made simultaneously in the three
operations.
(a) If the availabilities of operations
1,2, and 3 are changed to 438,500, and 410 minutes, respectively, use the
simultaneous conditions to show that the current basic solution remains
feasible, and determine the change in the optimal revenue by using the optimal
dual prices.
(b) If
the availabilities of the three operations are changed to 460,440, and 380
minutes, respectively, use the simultaneous conditions to show that the current
basic solution becomes infeasible.
*2. Consider the TOYCO model.
(a) Suppose that any additional time for
operation 1 beyond its current capacity of 430 minutes per day must be done on
an overtime basis at $50 an hour. The hourly cost includes both labor and the
operation of the machine. Is it economically advantageous to use overtime with
operation I?
(b) Suppose that the operator of operation 2
has agreed to work 2 hours of overtime daily at $45 an hour. Additionally, the
cost of the operation itself is $10 an hour. What is the net effect of this
activity on the daily revenue?
(c) Is overtime needed for operation 3?
(d) Suppose
that the daily availability of operation 1 is increased to 440 minutes. Any
overtime used beyond the current maximum capacity will cost $40 an hour.
Deter-mine the new optimum solution, including the associated net revenue.
(e) Suppose
that the availability of operation 2 is decreased by 15 minutes a day and that
the hourly cost of the operation during regular time is $30. Is it advantageous
to decrease the availability of operation 2?
3. A
company produces three products, A, B, and C. The sales volume for A is at
least 50% of the total sales of all three products. However, the company cannot
sell more than 75 units of A per day. The three products use one raw material,
of which the maxi-mum daily availability is 240 lb. The usage rates of the raw
material are 2 lb per unit of A,4 lb per unit of B, and 3lb per unit of C. The
unit prices for A, B, and Care $20, $50, and $35, respectively.
(a) Determine
the optimal product mix for the company.
(b) Determine
the dual price of the raw material resource and its allowable range. If
available raw material is increased by 120 lb, determine the optimal solution
and the change in total revenue using the dual price.
(c) Use
the dual price to determine the effect of changing the maximum demand for
product A by ± 10 units.
4. A
company that operates 10 hours a day manufactures three products on three
sequential processes. The following table summarizes the data of the problem:

(a) Determine the optimal product mix.
(b) Use the dual prices to prioritize the three
processes for possible expansion.
(c) If additional production hours can be
allocated, what would be a fair cost per additional hour for each process?
5. The
Continuing Education Division at the Ozark Community College offers a total of
30 courses each semester. The courses offered are usually of two types:
practical, such as wood-working, word processing, and car maintenance; and
humanistic, such as history, music, and fine arts. To satisfy the demands of
the community, at least 10 courses of each type must be offered each semester.
The division estimates that the revenues of offering practical and hu-manistic
courses are approximately $1500 and $1000 per course, respectively.
a. Devise
an optimal course offering for the college.
b. Show
that the dual price of an additional course is $1500, which is the same as the
revenue per practical course. What does this result mean in temlS of offering
addi-tional courses?
c. How
many more courses can be offered while guaranteeing that each will contribute
$1500 to the total revenue?
d. Determine
the change in revenue resulting from increasing the minimum requirement of
humanistics by one course.
*6. Show
& Sell can advertise its products on local radio and television (TV), or in
newspa-pers. The advertising budget is limited to $10,000 a month. Each minute
of advertising on radio costs $15 and each minute on TV costs $300. A newspaper
ad costs $50. Show & Sell likes to advertise on radio at least twice as
much as on TV. In the
meantime, the use of at least 5 newspaper ads and no more than 400 minutes of
radio advertising a month is recommended. Past experience shows that
advertising on TV is 50 times more effective than on radio and 10 times more
effective than in newspapers.
a. Determine
the optimum allocation of the budget to the three media.
b. Are
the limits set on radio and newspaper advertising justifiable economically?
c. If the monthly budget is increased
by 50%, would this result in a
proportionate in-crease in the overall effectiveness of advertising?
7. The
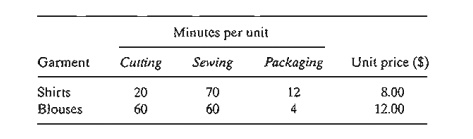
Burroughs Garment Company manufactures men's shirts and women's blouses for
Walmark Discount Stores. Walmark will accept all the production supplied by
Burroughs. The production process includes cutting, sewing, and packaging.
Burroughs employs 25 workers in the cutting department, 35 in the sewing
department, and 5 in the
packaging department. The factory works one 8-hour shift, 5 days a week. The
following table gives the time requirements and prices per unit for the two
garments:
a. Determine
the optimal weekly production schedule for Burroughs.
b. Determine
the worth of one hour of cutting, sewing, and packaging in terms of the total
revenue.
c. If overtime can be used in cutting
and sewing, what is the maximum hourly rate Bur-roughs should pay for overtime?
8. ChemLabs
uses raw materials I and II to produce two domestic cleaning
solutions, A and B. The daily availabilities of raw materials I and II are 150 and 145
units, respectively. One unit of
solution A consumes .5 unit of raw materiall and .6 unit of raw materialll, and
one unit of solution Buses .5 unit of
raw materiall and .4 unit of
raw materialll. The prices per unit of solutions A and Bare $8 and $10,
respectively. The daily demand for so-lution A lies between 30 and 150 units,
and that for solution B between 40 and 200 units.
a. Find
the optimal amounts of A and B that ChemLab should produce.
b. Use
the dual prices to determine which demand limits on products A and B should
be relaxed to improve profitability.
c. If additional units of raw material
can be acquired at $20 per unit, is this advisable? Explain.
d. A
suggestion is made to increase raw material II by 25% to remove a bottleneck in
production. Is this advisable? Explain.
9. An
assembly line consisting of three consecutive workstations produces two radio
models: DiGi-l and DiGi-2. The following table provides the assembly times for
the three workstations.
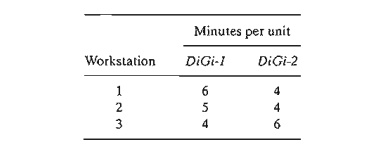
The daily
maintenance for workstations 1,2, and 3 consumes 10%,14%, and 12%,
re-spectively, of the maximum 480 minutes available for each workstation each
day.
a. The
company wishes to determine the optimal product mix that will minimize the idle
(or unused) times in the three workstations. Determine the optimum utilization of
the workstations. [Hint; Express the
sum of the idle times (slacks) for the three operations in terms of the
original variables.]
b. Determine
the worth of decreasing the daily maintenance time for each workstation by 1
percentage point.
c. It is proposed that the operation
time for all three workstations be increased to 600 minutes per day at the additional
cost of $1.50 per minute. Can this proposal be im-proved?
10. The
Gutchi Company manufactures purses, shaving bags, and backpacks. The
construc-tion of the three products requires leather and synthetics, with
leather being the limiting raw material. The production process uses two types
of skilled labor: sewing and finishing. The following table gives the
availability of the resources, their usage by the three products, and the
prices per unit.
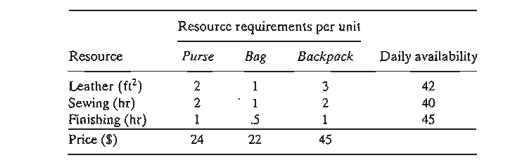
Formulate
the problem as a linear program and find the optimum solution. Next, indicate
whether the following changes in the resources will keep the current solution
feasible.
For the
cases where feasibility is maintained, determine the new optimum solution
(values of the variables and the objective function).
a. Available
leather is increased to 45 ft2•
b. Available
leather is decreased by 1 ft2•
c. Available sewing hours are
changed to 38 hours.
d. Available
sewing hours are changed to 46 hours.
e. Available
finishing hours are decreased to 15 hours.
f. Available
finishing hours are increased to 50 hours.
g. Would
you recommend hiring an additional sewing worker at $15 an hour?
11. HiDec
produces two models of electronic gadgets that use resistors, capacitors, and
chips. The following table summarizes the data of the situation:

Let x1 and x2 be the amounts produced of
Models 1 and 2, respectively. Following are the LP model and its associated
optimal simplex tableau.

*(a) Determine
the status of each resource.
*(b) In
terms of the optimal revenue, determine the dual prices for the resistors,
capaci-tors, and chips.
(c) Determine
the feasibility ranges for the dual prices obtained in (b).
(d) If
the available number of resistors is increased to 1300 units, find the new
optimum solution.
*(e) If the available number of chips is
reduced to 350 units, will you be able to deter-mine the new optimum solution
directly from the given information? Explain.
(f) If the availability of capacitors is
limited by the feasibility range computed in (c), determine
the corresponding range of the optimal revenue and the corresponding ranges for
the numbers of units to be produced of Models 1 and 2.
(g) A new
contractor is offering to sell HiDec additional resistors at 40 cents each, but
only if HiDec would purchase at least 500 units. Should HiDec accept the offer?
12. The 100% feasibility rule. A
simplified rule based on the individual changes D1,D2…... , and Dm in the right-hand side of the
constraints can be used to test whether or not simultaneous changes will maintain the feasibility of the current
solution. Assume that the right-hand
side bj of constraint i is changed to bi + D; one at a time, and that Pi≤ Di ≤ qj is the corresponding feasibility
range obtained by using the procedure in Section 3.6.2. By definition, we have Pi ≤; 0 (qj≥ 0) because it represents the
maximum allowable decrease (increase) in bi.
Next, define r1 to equal D1/P1 if Dj is negative and Di/qi if Di is positive. By definition, we
have 0 ≤ r1 ≤ 1. The
100% rule thus says that, given the changes

In
reality, the 100% rule is too weak to be consistently useful. Even in the cases
where feasibility can be confirmed, we still need to obtain the new solution
using the regular simplex feasibility conditions. Besides, the direct
calculations associated with simultane-ous changes given in Section 3.6.2 are
straightforward and manageable.
To
demonstrate the weakness of the rule, apply it to parts (a) and (b) of Problem
1 in this set. The rule fails to confirm the feasibility of the solution in (a)
and does not apply in (b) because the changes in Dj arc outside the admissible
ranges. Problem 13 further demonstrates this point.
13. Consider the problem
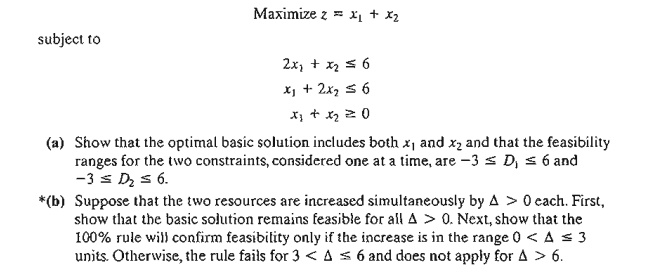
Related Topics