Selection sort

SELECTION SORT

Definition:

Selection sort or push-down sort implements selection phase in which either largest or smallest element find from the list and it is swapped to the last or first position respectively.

Algorithm:

The algorithm works as follows:

1.     Find the largest value in the list

2.     Swap it with the value in the last position

3.     Repeat the steps above for the remainder of the list (starting at the second position and advancing each time)

Implementation in C:

#include <stdio.h> #include<conio.h> void main()

{

int array[100], n, c, d, position, swap; printf("Enter number of elements\n"); scanf("%d", &n);

printf("Enter %d integers\n", n); for ( c = 0 ; c < n ; c++ )

scanf("%d", &array[c]);

for ( c = 0 ; c < ( n - 1 ) ; c++ )

{

position = c;

for ( d = c + 1 ; d < n ; d++ )

{

if ( array[position] > array[d] ) position = d;

}

if ( position != c )

{

swap = array[c];

array[c] = array[position]; array[position] = swap;

}

}

printf("Sorted list in ascending order:\n"); for ( c = 0 ; c < n ; c++ )

printf("%d\n", array[c]); getch();

}

Execution:

For example, consider the following array, shown with array elements in sequence separated by commas:

The leftmost element is at index zero, and the rightmost element is at the highest array index, in our case, 4 (the effective size of our array is 5).

The largest element in this effective array (index 0-4) is at index 2. We have shown the largest element and the one at the highest index in bold. We then swap the element at index 2 with that at index 4. The result is:

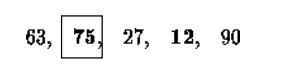
We reduce the effective size of the array to 4, making the highest index in the effective array now 3. The largest element in this effective array (index 0-3) is at index 1, so we swap elements at index 1 and 3 (in bold):

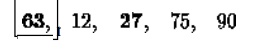
The next two steps give us:

Now the list is sorted.

Complexity Analysis:

Selection sort is not difficult to analyze compared to other sorting algorithms since none of the loops depend on the data in the array.

Selecting the lowest element requires scanning all n elements (this takes n −1 comparisons) and then swapping it into the first position.

Finding the next lowest element requires scanning the remaining n −1 elements and so on, ∈ for (n −1) + (n −2) + ... + 2 + 1 = n(n −1) / 2   Θ(n) comparisons.

Insertion Sorts

•      A simple sorting technique that scans the sorted list, starting at the beginning, for the correct insertion point for each of the items from the unsorted list.

•      Similar to the way people manually sort items, an insertion sort is not efficient for large lists, but is relatively fast for adding a small number of new items periodically.

Three insertion sort related sorting techniques are discussed here they are

i)                   Simple Insertion Sort

ii)                Shell sort

iii)              Address Calculation sort.