Bubble sort

BUBBLE SORT:

Bubble sort is a simple sorting algorithm. The algorithm starts at the beginning of the data set. It compares the first two elements, and if the first is greater than the second, it swaps them.

It continues doing this for each pair of adjacent elements to the end of the data set. It then starts again with the first two elements, repeating until no swaps have occurred on the last pass.

Bubble sort can be used to sort a small number of items (where its inefficiency is not a high penalty). Bubble sort may also be efficiently used on a list that is already sorted except for a very small number of elements.

For example, if only one element is not in order, bubble sort will take only 2n time. If two elements are not in order, bubble sort will take only at most 3n time.

Bubble Sort Algorithm:

#include<stdio.h>

#include<conio.h>

void main( )

{

int a[100];

int i, j, temp, n ;

printf("how many numbers you want to sort : \n"); scanf("%d",&n);

printf("Enter %d number values you want to sort\n", n); for(j=0; j<n; j++)

scanf("%d",&a[j]);

for(j=1;j<n;j++)

{

for(i=0; i<n; i++)

{

if(a[i]>a[i+1])

{

temp=a[i];

a[i]=a[i+1];

a[i+1]=temp;

}

}

}

printf ( "\n\nArray after sorting:\n") ;

for ( i = 0 ; i <n ; i++ ) printf ( "%d\t", a[i] ) ; getch();

}

Algorithm Explanation

•         Traverse a collection of elements

– Move from the front to the end

 – “Bubble” the largest value to the end using pair-wise comparisons and swapping.

– After the first traversal only the largest value is correctly placed

– All other values are still out of order

– So we need to repeat this process.

–   – If we have N elements… And if each time we bubble an element, we place it in its correct location…

– Then   we   repeat   the–1 times“bubble.   up”   process

– This   guarantees   we’ll   correctly   place   a

•         We can use a Boolean variable (Here it is switched) to determine if any swapping occurred during the “bubble up.”

•         If no swapping occurred, then we know that the collection is already sorted.

•         This   Boolean   “flag”   needs   to   be   reset   afte

Execution of Algorithm:

The given input values are

Pass 0

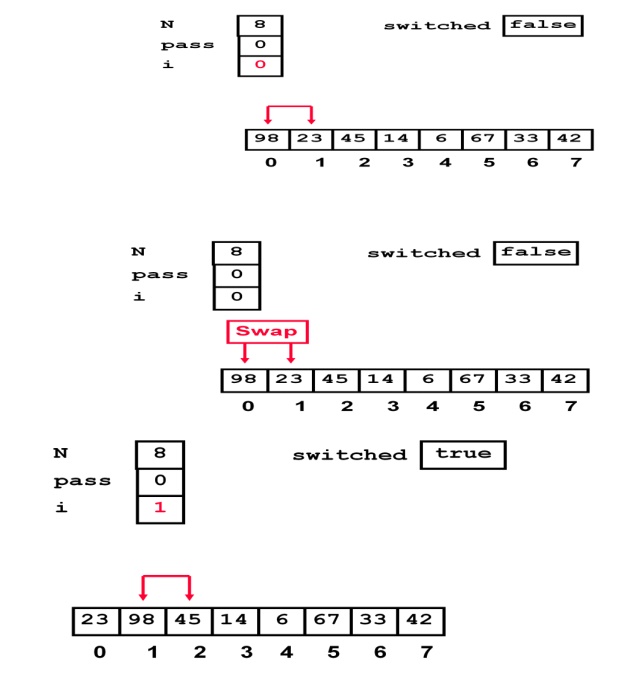
Like wise the iterations will continue for the Pass 0 with adjacent values comparisons and swapping. Finally after I pass that pass 0 the list will look as follows..

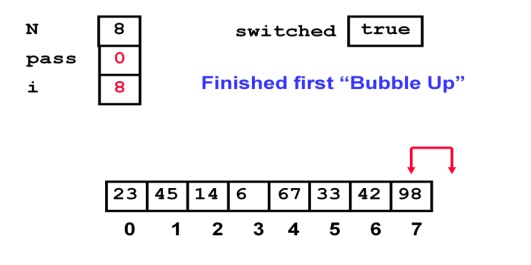
Now the last element will freeze out. That is it will not get considered for the next passes. Such that for each passes one element will get frozen out. The pass will get over if the elements

haven’t swapped for a complete iteration. It variable. It will be false if swapping not happened.

Efficiency Analysis of Bubble sort:

•      One traversal = move the maximum element at the end

•      Traversal : n –i + 1 operations

•      Running time:

 (n –1) + (n –2)   +   …   +   1   =   (n)by applying+1)the summation/ 2formula=. O(n)