Chapter: Programming and Data Structures : Sorting And Searching
Merge sort
MERGE SORT
Definition;
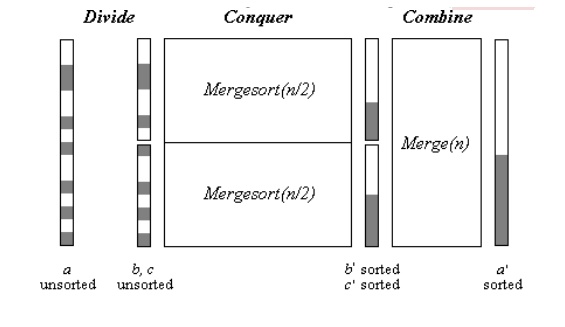
The Merge sort
algorithm is based on divide and conquers strategy. First, the sequence to be
sorted is decomposed into two halves ( Divide
). Each half is sorted independently ( Conquer
). Then the two sorted halves are merged to a sorted sequence ( Combine ).
Algorithm:
The following procedure merge sort sorts a
sequence a from index min to index max.
#include<stdio.h>
#include<conio.h>
void merge(int [],int ,int ,int );
void part(int [],int ,int );
int main()
{
int
arr[30];
int
i,size;
printf("\n\t-------
Merge sorting method -------\n\n");
printf("Enter
total no. of elements : ");
scanf("%d",&size);
for(i=0;
i<size; i++)
{
printf("Enter
%d element : ",i+1);
scanf("%d",&arr[i]);
}
part(arr,0,size-1);
printf("\n\t-------
Merge sorted elements -------\n\n");
for(i=0;
i<size; i++)
printf("%d
",arr[i]);
getch();
return
0;
}
void part(int arr[],int min,int max)
{
int
mid;
if(min<max)
{
mid=(min+max)/2;
part(arr,min,mid);
part(arr,mid+1,max);
merge(arr,min,mid,max);
}
}
First, index m in the middle
between lo and hi is determined. Then the first part of the
sequence (from lo to m) and the second part (from m+1 to hi)
are sorted by recursive calls of merge sort. Then the two sorted halves
are merged by procedure merge. Recursion ends when lo = hi,
i.e. when a subsequence consists of only one element.
The main work of the
Merge sort algorithm is performed by function merge. There are different
possibilities to implement this function.
The Merge method defined as follows,
void merge(int arr[],int min,int mid,int max)
{
int
tmp[30];
int
i,j,k,m;
j=min;
m=mid+1;
for(i=min;
j<=mid && m<=max ; i++)
{
if(arr[j]<=arr[m])
{
tmp[i]=arr[j];
j++;
}
else
{
tmp[i]=arr[m];
m++;
}
}
if(j>mid)
{
for(k=m; k<=max; k++)
{
tmp[i]=arr[k];
i++;
}
}
else
{
for(k=j;
k<=mid; k++)
{
tmp[i]=arr[k];
i++;
}
}
for(k=min;
k<=max; k++)
arr[k]=tmp[k];
}
This variant of
function merge requires in each case exactly the same number of steps
–no matter if the input sequence is random, sorted or sorted in opposite
direction.
Execution:
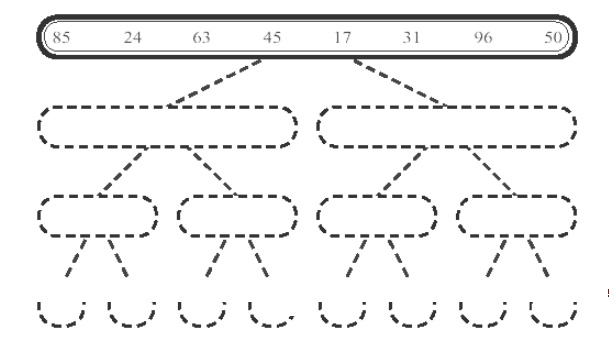

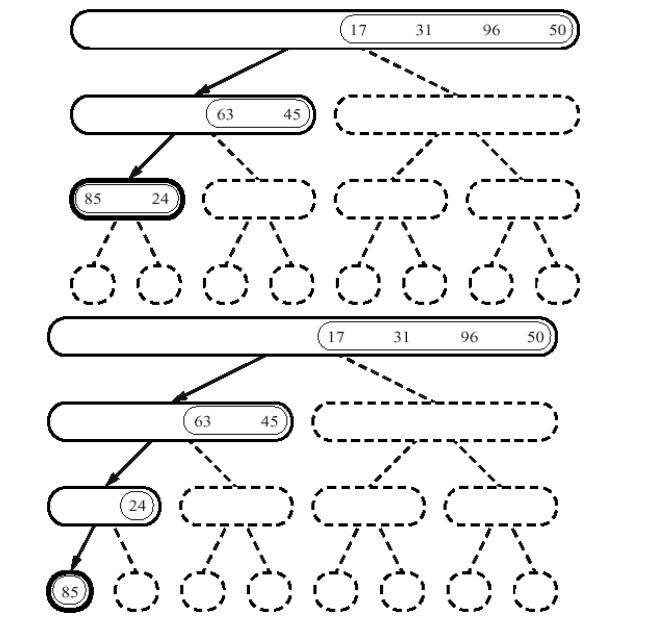
Just like the above
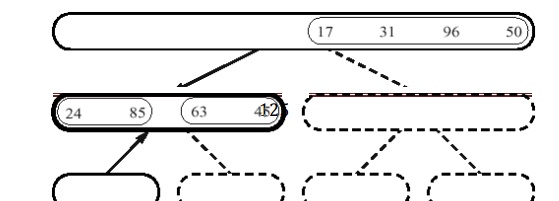
steps the second recursion will sort the sequence at the right hand side.
Finally the both partitioned sorted sub arrays are get merged in the sorted
sequence.
The final merging steps are as follows,
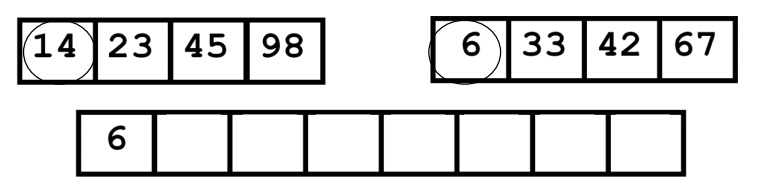
14 and 6 are compared and 6 placed in the first
position.
Next comparison will be
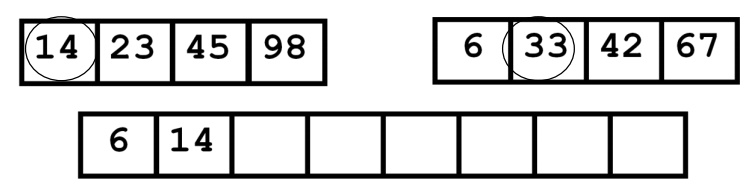
Now comparing 14 and 33 14 is least
value so place it in the second place. Next comparison,
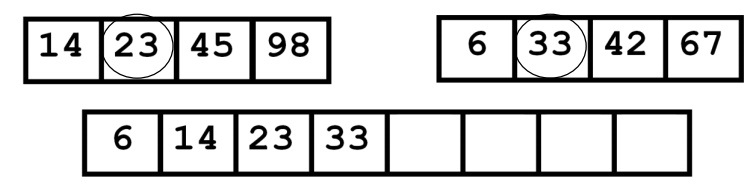
Likewise the comparisons done till
reaches the end of the sub arrays and the list will be sorted at last, the
sorted list will be as follows,

Complexity Analysis:
The straightforward version of function merge requires at most 2n steps (n steps for copying the sequence to the intermediate array b, and at most n steps for copying it back to array a). The time complexity of merge sort is therefore
T(n) < = 2n
+ 2 T(n/2) And
T(1) = 0
The solution
of this recursion yields
T(n) < = 2n log(n) include O(n log(n))
Thus, the merge sort algorithm is optimal, since the lower bound for the sorting problem of Ω (n log (n)) is attained.
In the more efficient variant, function merge
requires at most 1.5n steps (n/2 steps for copying the first half
of the sequence to the intermediate array b, n/2 steps for
copying it back to array a, and at most n/2 steps for processing
the second half). These yields a running time of merge sort of at most
1.5n log (n) steps.
Related Topics