Quick sort

QUICK SORT

A sorting technique that sequences a list by continuously dividing the list into two parts and moving the lower items to one side and the higher items to the other. It starts by picking one item in the entire list to serve as a pivot point.

The pivot could be the first item or a randomly chosen one. All items that compare lower than the pivot are moved to the left of the pivot; all equal or higher items are moved to the right.

It then picks a pivot for the left side and moves those items to left and right of the pivot and continues the pivot picking and dividing until there is only one item left in the group. It then proceeds to the right side and performs the same operation again. Also known as Partition

 Exchange Sort.

Quick sort algorithm applies a special designing technique called Divide and Conquer,

The divide-and-conquer strategy solves a problem by:

1. Breaking it into sub problems that are themselves smaller instances of the same type of problem

2. Recursively solving these sub problems

3. Appropriately combining their answers

Divide and Conquer in Quick sort

Divide: If the sequence S has 2 or more elements, select an element x from S to be your pivot. Any arbitrary element, like the last, will do. Remove all the elements of S and divide them into 3 sequences:

L, holds S’s elements less than x E, holds S’s elements equal to x

G,      holds   S’s   elements   greater   than   x

2) Recurse: Recursively sort L and G

3)  Conquer: Finally, to put elements back into S in order, first inserts the elements of L, then those of E, and those of G.

Step 1: Select: pick an element

Step 2: Divide: rearrange elements so that x goes to its final position E

Step 3: Recurse and conquer: recursively sort

Quick Sort Algorithm:

#include<stdio.h>

#include<conio.h>

void qsort(int arr[20], int left, int right); int main()

{

int arr[30]; int i,n;

printf("Enter total no. of the elements : ");

scanf("%d",&n);

printf("Enter total %d elements : \n",size); for(i=0; i<n; i++)

scanf("%d",&arr[i]); qsort(arr,0,n-1);

printf("Quick sorted elements are as : \n"); for(i=0; i<n; i++)

printf("%d\t",arr[i]);

getch(); return 0;

}

void qsort(int arr[20], int left, int right)

{

int i,j,pivot,tmp; if(left<right)

{

pivot=left;

i=left+1;

j=right;

while(i<j)

{

while(arr[i]<=arr[pivot] && i<right) i++;

while(arr[j]>arr[pivot]) j--;

if(i<j)

{

tmp=arr[i];

arr[i]=arr[j];

arr[j]=tmp;

}

}

tmp=arr[pivot];

arr[pivot]=arr[j];

arr[j]=tmp; qsort(arr,left,j-1); qsort(arr,j+1,right);

}

}

The partition method uses two while statements one is for incrementing the variable to arrange the sequence in left side with least values. Another while statement for decrementing the variable to arrange the sequence in right side with greatest values when compared with the pivot element.

Execution for Partition method:

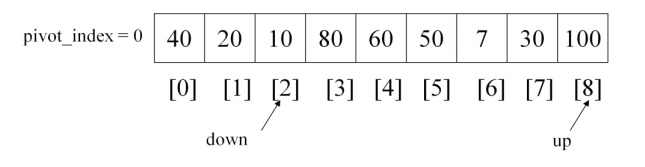
There are a number of ways to pick the pivot element. In this example, we will use the first element in the array

Compare 20 and pivot element 40 the 20 is least value so down alone get incremented.

Again compare pivot element and element pointing down, 10 is least value again so down value get incremented.

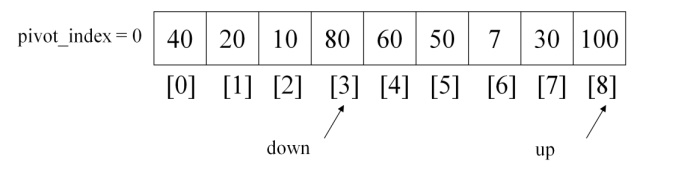
But Here the situation is 80 value pointed by down index is high when compared with the pivot element. So 1^st while statement get terminated.

Now, up value will start to get decremented. The array will be as follows

Up value will get decrement if the value pointing up is greater than pivot element, but now the situation is up pointing element is least when compared with the pivot element. So now second while also get terminated.

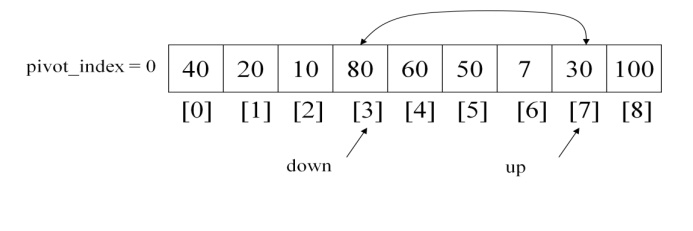
Now after the end of two while statements if down is less than up swap these two values to arrange left sub array with least values in the left side of the pivot element and greatest values at the right side of the pivot element.

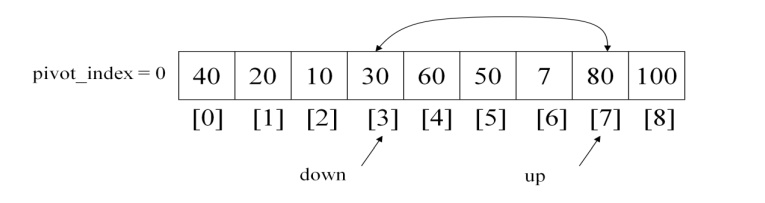
Continue the two whiles again and find two values to get swapped until down < up

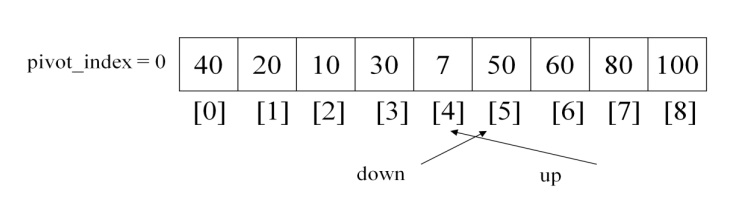
So now stop the iteration and swap the pivot element towards the up position like below.

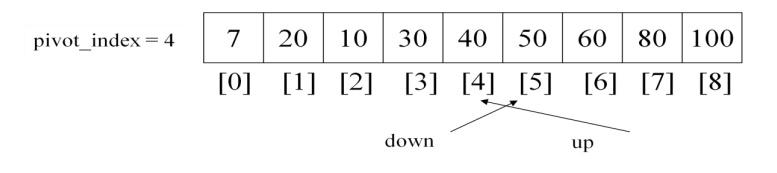
Current pivot index has been updated with the value 4 and the pivot element also swapped to the pivot index.

These Sub arrays are now again introduced into the partition with the above steps. The two sub arrays are from 0 to 3 and 4 to 8. So the first sub array again partitioned into two, depending upon pivot element position. The quick sort procedure with the partition method is as follows.

void quicksort ( int a[ ], int left, int right )

{

int mid;

if ( right > left )

{

mid = quicksort (a, left, right) ; quicksort ( a, left, mid - 1 ) ; quicksort ( a, mid+ 1, right ) ;

}

}

Here the variable i is the partition index. And accordingly the quick sort performs two partitions each time depending upon the pivot index.

Complexity Analysis:

o   Recursion:

^§    Partition splits array in two sub-arrays of size n/2

^§    Quick sort each sub-array

o  Depth of recursion tree O(log₂n)

o Number of accesses in partition O(n)

Assume that keys are random, uniformly distributed.

Best case running time: O(n log₂n)

The Master theorem can be applied to calculate the efficiency. The theorem is as follows,

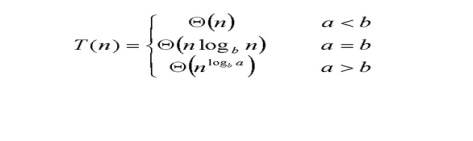
For the Quick sort the standard format is T(n) = aT(n/b)+F(n)

Where a and b are Number of recursions and number of partitions respectively.

For quick sort a=2 and b=2, so a and b are equal so the efficiency is θ   (n   log   n)

Selection sorts

Selection sort is a sorting algorithm, specifically an in-place comparison sort. It has O (n2) time complexity, making it inefficient on large lists, and generally performs worse than the similar insertion sort.

Selection sort is noted for its simplicity, and also has performance advantages over more complicated algorithms in certain situations, particularly where auxiliary memory is limited.

Three types of selection sorts are discussed here,

i)                  Straight Selection sort

ii)                Binary tree Sort

iii)             Heap sort