Search Algorithm: Linear search or sequential search and Binary search

SEARCHING:

Search Algorithm:

A search algorithm is an algorithm that accepts an argument and tries to find a record whose key is  ‘a’. The algorithm may return the entire re record.

Basic Terminologies:

File: A table or file is group of elements.

Record: Each field in a table or file is known as record.

Key: Associated with each record, which is used to differentiate among different records.

Three different keys,

Internal Key: The key is contained within the record at a specific offset from the start of the record, such a key is Internal or Embedded key.

External Key: There is a separate table of keys that includes pointers to the records. Such keys are External keys.

Primary Key: For every file or table there is at least one set of a key that is unique.

Secondary Key: For a table or file if searching done on the record which is not unique such a key is secondary key.

Records and Keys

Internal search: Searching key data stored in main memory

External search: Searching key data stored in auxiliary memory

Retrieval: Output of a successful search

1SEQUENTIAL SEARCHING:

Each searching function has two input parameters:

1.     First is the list to be searched;

2.     Second is the target key for which we are searching.

Each searching function will also have an output parameter and a returned value:

The returned value has type Error code and indicates whether or not the search is successful in appending an entry with the target key.

If the search is successful, then the returned value is success, and the output parameter called position will locate the target within the list.

If the search is unsuccessful, then the value not present is returned and the output parameter may have an undefined value or a value that will differ from one method to another.

Definition:

Linear search or sequential search is a method for finding a particular value in a list that consists of checking every one of its elements, one at a time and in sequence, until the desired one is found. Linear search is the simplest search algorithm; it is a special case of brute-force search.

Algorithm:

#include<stdio.h>

main()

{

int array[100], search, c, number;

printf("Enter the number of elements in array\n"); scanf("%d",&number);

printf("Enter %d numbers\n", number);

for ( c = 0 ; c < number ; c++ ) scanf("%d",&array[c]);

printf("Enter the number to search\n"); scanf("%d",&search);

for ( c = 0 ; c < number ; c++ )

{

if ( array[c] == search )   /* if required element found */

{

printf("%d is present at location %d.\n", search, c+1); break;

}

}

if ( c == number )

printf("%d is not present in array.\n", search);

return 0;

}

This search is applicable to a table organized either as an array or as a linked list. The algorithm examines each key in turn upon finding one that matches the search argument, its index is returned. If no match found -1 is returned.

For efficient searching algorithm we can add a node called sentinel node an extra key inserted at the end of the array.

k[n] = key;

for (i = 0; key != k[i]; i++) ; if (i < n) return(i);

else return(-1);

Let p (i) be the probability that record i is retrieved.

p(0)+ p(1)+ ... + p(n-1) = 1. Average number of comparisons:

p(0) + 2p(1) + 3p(2) + ... + np(n-1) This number is minimized if

p(0) ≧p(1) ≧p(2) ≧... ≧p(n-1).

Reordering a List for Maximum Search Efficiency

There are two search methods that accomplish the maximum searching efficiency are

i)                   Move to Front

ii)                Transposition Method.

Move to Front:

In this method whenever a search is successful the retrieved record is removed from its current location in the list and is placed at the head of the list.

e.g. 9 5 6 8 7 2

(1) search 6:   6 9 5 8 7 2

(2) search 8:   8 6 9 5 7 2

The retrieved record is moved to the head of the list.

Searching in an ordered table

If the table is in ascending or descending order of the record keys, then there are several techniques that can be used to improve the efficiency of searching.

An obvious advantage in searching a sorted file is in the case that the argument keys are uniformly distributed over in the case if records are not sorted the comparisons needed are n. for a sorted sequence the comparisons needed are n/2.

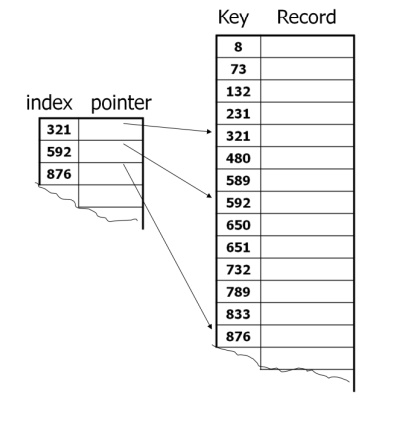
The Indexed sequential Search:

It is another method to improve the efficiency of searching in a sorted list. An auxiliary table called an index is set aside in addition to the sorted file itself.

But it needs extra space; this method is also known as indexed sequential method. Let r, k and key be three input values of this algorithm. Other values are kindex be an array of keys in the index, and let pindex be the array of pointers with in the index.

Indxsize size of the index table. N number of records in the main table.

Deletion is done by flagging. Through that if the flag is set, the record can be ignored. Insertion is more difficult because it is necessary to shift all the records to make room for the new record.

If the table is so large a single index cannot be sufficient to achieve efficiency. So we can maintain secondary index.

The secondary index acts as an index to the primary index. Which will points entry to the sequential table.

2 BINARY SEARCH:

Definition:

A dichotomizing search in which the set of items to be searched is divided at each step into two equal, or nearly equal, parts, Also known as binary chop.

The most efficient method used for searching a seq any primary or secondary index.

Algorithm Explanation:

A binary search or half-interval search algorithm finds the position of a specified value (the input "key") within a sorted array. At each stage, the algorithm compares the input key value with the key value of the middle element of the array.

·        If the keys match, then a matching element has been found so its index, or position, is returned.

·        Otherwise, if the sought key is less than the middle element's key, then the algorithm repeats its action on the sub-array to the left of the middle element or,

·        if the input key is greater, on the sub-array to the right. If the remaining array to be searched is reduced to zero, then the key cannot be found in the array and a special "Not found" indication is returned.

#include<stdio.h>

#include<conio.h> void main(){

int a[10],i,n,m,c=0,l,u,mid;

printf("Enter the size of an array: "); scanf("%d",&n);

printf("Enter the elements in ascending order: "); for(i=0;i<n;i++){

scanf("%d",&a[i]);

}

printf("Enter the number to be search: "); scanf("%d",&m);

l=0,u=n-1; while(l<=u){

mid=(l+u)/2;

if(m==a[mid]){

c=1;

break;

}

else if(m<a[mid])

{

u=mid-1;

}

else l=mid+1;

}

if(c==0)

printf("The number is not found."); else

printf("The number is found.");

getch();

}

Example:

For example, consider the following sequence of integers sorted in ascending order and say we are looking for the number 55:

The search space contains indices 0 through 10 respective low and high indices As described above, we now choose the mid value 0 + 10 /2 =5

The value is in the location 5 is 41 and it is smaller than the target value.

From this we conclude not only that the element at index 5 is not the target value, but also that no element at indices between 0 and 5 can be the target value, because all elements at these indices are smaller than 41, which is smaller than the target value. This brings the search space down to indices 6 through 10:

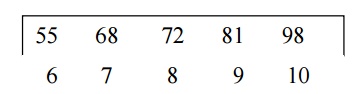
Proceeding in a similar fashion, we chop off the second half of the search space and are left with: (6+10/2 = 8 mid value in 8 is 72 which is greater than 55 so the indices are 6 and 7.

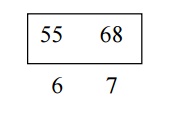
Depending on how we choose the median of an even number of elements we will either find 55 in the next step or chop off 68 to get a search space of only one element. Either way, we conclude that the index where the target value is located is 7.

Efficiency Analysis:

That is, which of the following will first be < 1? < n/2, n/4, n/8, n/16, ..., n/2k, ...

We solve the equation: n/2k < 1, and get k > log2n So if we set k = [log2n] , then we know that after that many iterations of the while loop, we will have found our item, or concluded that it was not in the list.