Resting Membrane Potential of Nerves

Resting Membrane Potential of Nerves

The resting membrane potential of large nerve fibers when not transmitting nerve signals is about –90 millivolts. That is, the potential inside thefiber is 90 millivolts more negative than the potential in the extra-cellular fluid on the outside of the fiber. In the next few paragraphs, we explain all the factors that determine the level of this resting potential, but before doing so, we must describe the transport properties of the resting nerve membrane for sodium and potassium.

Active Transport of Sodium and Potassium Ions Through the Membrane—The Sodium-Potassium (Na+-K+) Pump. First, letus recall that all cell membranes of the body have a powerful Na+-K+ that continually pumps sodium ions to the outside of the cell and potassium ions to the inside, as illustrated on the left-hand side in Figure 5–4. Further, note that this is an electrogenicpump because more positive charges are pumped tothe outside than to the inside (three Na+ ions to the outside for each two K+ ions to the inside), leaving a net deficit of positive ions on the inside; this causes a negative potential inside the cell membrane.

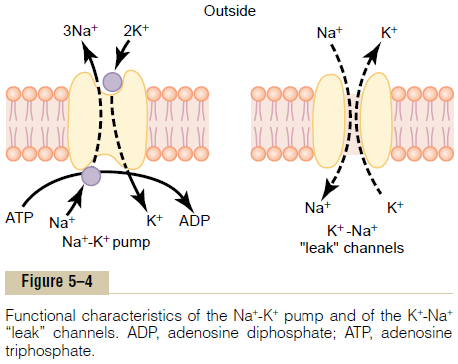
The Na+-K+ also causes large concentration gradi-ents for sodium and potassium across the resting nerve membrane. These gradients are the following:

The ratios of these two respective ions from the inside to the outside are

        Na+inside/Na+outside = 0.1

        K+inside/K+outside = 35.0

Leakage of Potassium and Sodium Through the Nerve Mem- brane. The right side of Figure 5–4 shows a channelprotein in the nerve membrane through which potas-sium and sodium ions can leak, called a potassium-sodium (K+-Na+) “leak” channel. The emphasis is onpotassium leakage because, on average, the channels are far more permeable to potassium than to sodium, normally about 100 times as permeable. As discussed later, this differential in permeability is exceedingly important in determining the level of the normal resting membrane potential.

Origin of the Normal Resting Membrane Potential

Figure 5–5 shows the important factors in the estab-lishment of the normal resting membrane potential of–90 millivolts. They are as follows.

Contribution of the Potassium Diffusion Potential. In Figure5–5A, we make the assumption that the only move-ment of ions through the membrane is diffusion of potassium ions, as demonstrated by the open channels between the potassium symbols (K+) inside and outside the membrane. Because of the high ratio of potassium ions inside to outside, 35:1, the Nernst

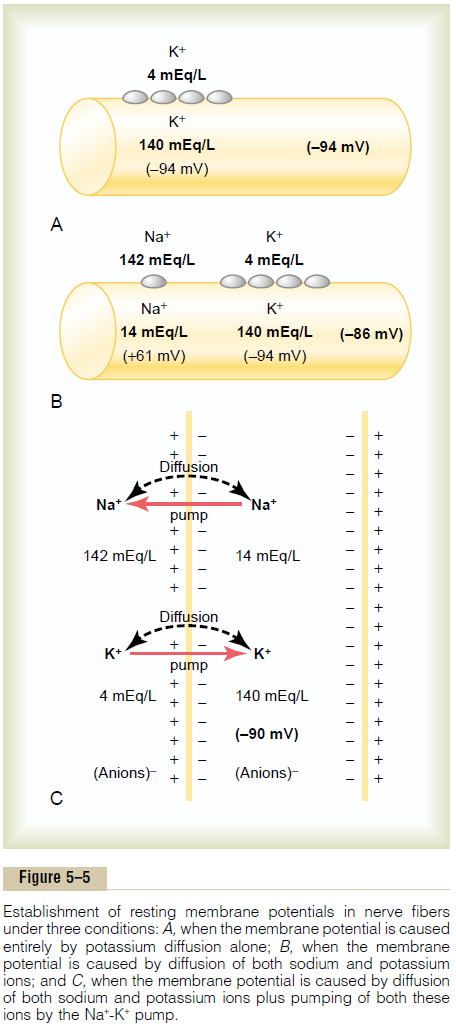
potential corresponding to this ratio is –94 millivolts because the logarithm of 35 is 1.54, and this times –61 millivolts is –94 millivolts. Therefore, if potassium ions were the only factor causing the resting potential, the resting potential inside thefiber would be equal to –94 millivolts, as shown in the figure.

Contribution of Sodium Diffusion Through the Nerve Membrane.

Figure 5–5B shows the addition of slight permeability of the nerve membrane to sodium ions, caused by the minute diffusion of sodium ions through the K+-Na+ leak channels. The ratio of sodium ions from inside to outside the membrane is 0.1, and this gives a calculated Nernst potential for the inside of the membrane of +61 millivolts. But also shown in Figure 5–5B is the Nernst potential for potassium diffusion of –94 milli-volts. How do these interact with each other, and what will be the summated potential? This can be answered by using the Goldman equation described previously. Intuitively, one can see that if the membrane is highly permeable to potassium but only slightly permeable to sodium, it is logical that the diffusion of potassium con-tributes far more to the membrane potential than does the diffusion of sodium. In the normal nerve fiber, the permeability of the membrane to potassium is about 100 times as great as its permeability to sodium. Using this value in the Goldman equation gives a potential inside the membrane of –86 millivolts, which is near the potassium potential shown in the figure.

Contribution of the Na+-K+ Pump. In Figure 5–5C, theNa+-K+ pump is shown to provide an additional con-tribution to the resting potential. In this figure, there is continuous pumping of three sodium ions to the outside for each two potassium ions pumped to the inside of the membrane. The fact that more sodium ions are being pumped to the outside than potassium to the inside causes continual loss of positive charges from inside the membrane; this creates an additional degree of negativity (about –4 millivolts additional) on the inside beyond that which can be accounted for by diffusion alone. Therefore, as shown in Figure 5–5C, the net membrane potential with all these factors operative at the same time is about –90 millivolts.

In summary, the diffusion potentials alone caused by potassium and sodium diffusion would give a mem-brane potential of about –86 millivolts, almost all of this being determined by potassium diffusion. Then, an additional –4 millivolts is contributed to the mem-brane potential by the continuously acting electro-genic Na+-K+ pump, giving a net membrane potential of –90 millivolts.