Regression

Regression

Evolution of Regression

The term ‘Regression’ was first coined and used in 1877 by Francis Galton while studying the relationship between the height of fathers and sons. The average height of children born of parents of a given height tended to move or “regress” toward the average height in the population as a whole. Galton’s law of universal regression was confirmed by his friend Karl Pearson, who collected more than a thousand records of heights of members of family groups. The literal meaning of the word “regression” is “Stepping back towards the average”.

Regression is the study of the relationship between the variables. If Y is the dependent variable and X is independent variable, the linear relationship between the variable is called the regression equation of Y on X, The regression equation is used to estimate the value of Y corresponding to the known value of X. The line describing this tendency to regress or going back was called by Galton a “Regression Line”.

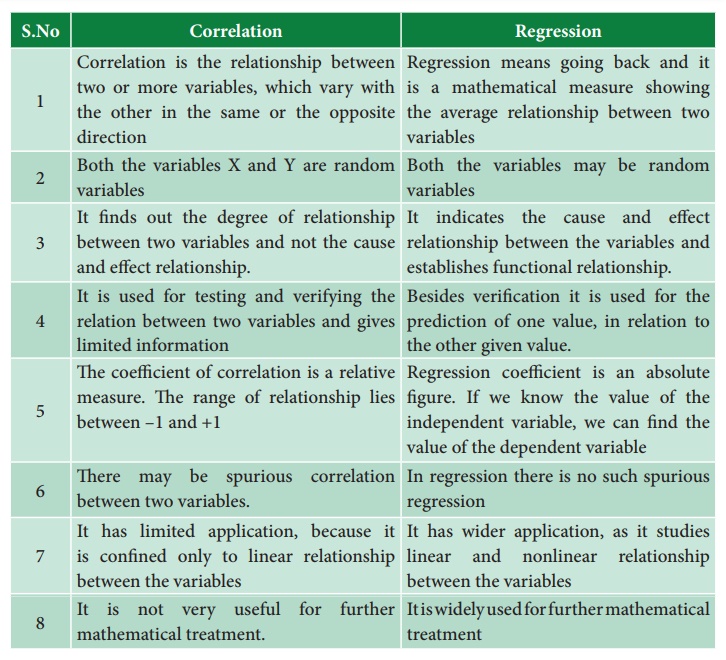
Difference between Correlation and Regression

Correlation

1. Correlation is the relationship between two or more variables, which vary with direction

2 Both the variables X and Y are random variables

3. It finds out the degree of relationship between two variables and not the cause and effect relationship.

4. It is used for testing and verifying the relation between two variables and gives limited information

5.  The coefficient of correlation is a relative measure. The range of relationship lies between –1 and +1

6. There may be spurious correlation between two variables.

7. It has limited application, because it is confined only to linear relationship between the variables

8. It is not very useful for further mathematical treatment.

Regression

1. Regression means going back and it is a mathematical measure showing the other in the same or the opposite the average relationship between two variables

2. Both the variables may be random variables

3. It indicates the cause and effect relationship between the variables and establishes functional relationship.

4. Besides verification it is used for the prediction of one value, in relation to the other given value.

5. Regression coefficient is an absolute figure. If we know the value of the  independent variable, we can find the  value of the dependent variable

6. In regression there is no such spurious regression

7. It has wider application, as it studies linear and nonlinear relationship between the variables

8. It is widely used for further mathematical treatment

Two Regression lines

X on Y => X = a + by

Y on X => Y = a + bx

Regression line is the line which gives  the best estimate of one variable from the value of any other given variable. The line gives  the  average  relationship  between the two variables in mathematical form. The line of regression is the line which gives the best estimate to the value of one variable for any specific value of the other variable.

To fit Regression equations X on Y and Y on X the following examples are given    

Ex 1: Fit two regression equation X on Y and Y on X for the following data.Xbar= 12, Ybar=10, σy= 0.2, σx =0.1 and r = 0.85

Solution

The regression X on Y is

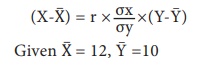
r = 0.85, σx = 0.1 and σy = 0.2

Then substituting the values in formula

Then substituting the values in formula

(X-12) = 0.85 × (0.1/0.2) × (Y-10)

(X-12) = 0.85 × (0.5) × (Y-10)

X = 0.425 ×(Y-10)+ 12

X = 0.425Y- 4.25+12

X = 0.425Y+7.75

X on Y

Answer X = 0.425Y + 7.75

The regression Y on X is

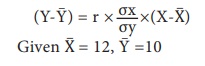
r = 0.85, σx = 0.1 and σy = 0.2

Then substituting the values in formula

(Y-10) = 0.85 × (0.2/0.1) × (X–12)

(Y-10) = 0.85 × (2) × (X–12)

Y = 1.7 × (X–12) + 10

Y = 1.7X–20.4+10

Y = 1.7X–10.4

Y on X

Answer Y = 1.7X–10.4