Plastic Bending

One Dimensional Plasticity for Design

In the previous pages, a full-range plasticity solution for an EPS thick ring was developed in detail to illustrate the fundamental concepts of plastic anal-ysis. This was possible only because a thick ring subjected to internal or exter-nal “pressure” is essentially a one-dimensional problem in that there is only one governing equilibrium equation since there is no variation of the field in the hoop direction. At any stage of plastic deformation, this equation can be integrated directly to determine the stress field. The strain and deformation field is then determined from the behavior of the elastic rim, which has not yet yielded.

The same is true for pure bending and the other one-dimensional linear elastic fields of previous pages. It is also possible to obtain full plasticity solutions in pure torsion for many cases considered in previous pages. Combinations of lin-ear fields can also be considered. Since limit analysis and design* of beams, shafts, frames, plates, and many other structural systems are based on these one-dimensional plasticity solutions, it is important to study them.

Plastic Bending

The basic assumption of the theory of flexure as stated in Section 5.5 is that plane sections normal to the axis of the beam remain plane so that the beam under pure bending deforms into a circle with radius of curvature ρ. This assumption as to the geometry of deformations has nothing to do with mate-rial properties and requires that longitudinal strains, E_x, in the fibers vary directly as their distance, y, from the neutral axis as given by Equation (5.15).

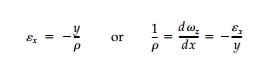
Thus, from equilibrium requirements, a general theory can be developed for bending beyond initial yield.*

Any prismatic beam with a cross-section with symmetry about a vertical axis can be considered. The neutral axis, defined as where the strain is zero, goes through the centroid in the elastic range but may migrate as the yield-ing progresses such that horizontal equilibrium is maintained. That is C = T or

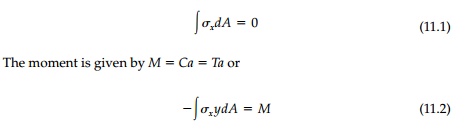
The solution of the general case of inelastic bending requires that these equi-librium Equations (11.1) and (11.2) for the given stress�'strain relationship be solved by trial and error. Two relatively simple cases are explored as chapter problems.

Let us consider only the case of a beam of an elastic, perfectly-plastic solid and start with a rectangular cross-section as shown in Figure 11.1. At yield of the outermost fibers, the moment M_Y = YI/c = Ybh²/6   = YS. As more moment is applied, the plastic zone moves toward the neutral axis and, because of our idealization of the material as an EPS, there is a sharp separa-tion leaving an elastic core at the center. If, for example, the strain at the outer surface is twice the yield strain,ϕ =2ϕ_Y, the middle half of the beam remains elastic (Figure 11.1b) and the moment works out to be 11/48 Ybh2. At very large rotations of the cross-section, as in Figure 11.1c, the linear distribution in the small elastic core can be neglected and the stress assumed as Y throughout. Thus, this ultimate or plastic moment is

Throughout, the neutral axis remains at mid-height because of the sym-metry around the z axis coupled with the requirement that the compres-sion force in the top equal the tension force in the bottom. The elastic section modulus, S, and plastic section modulus, Z, are given in various handbooks for standard shapes such as angles, channels, wideflange, and I beams. The ratio Z/S = M_P/M_y is often called the shape factor, K_s. For a rectangular cross-section then, K_s=1.5 indicating this shape has a large reserve capacity to take additional moment beyond yield because of its inefficiency in the elastic range. For WF and I beams, K_{s =} 1.12 and it takes only 12% more moment to fully plasticize the section as to yield it.

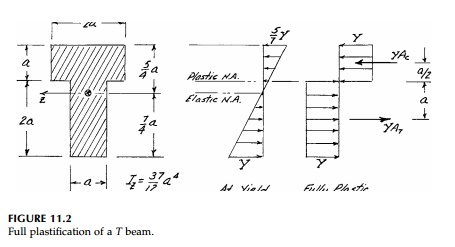
As a second example, consider the T beam in Figure 11.2. The moment of inertia about the centroidal axis I_z = (37/12) a⁴ and therefore the elastic yield moment:

As the moment increases beyond that necessary to yield the outermost fiber at the bottom, the neutral axis must shift upward since horizontal equilibrium requires that the compression in the top always equal the tension in the bottom. Finally, at full plastification, when all the fibers reach yield, C= YA_c = T = YA_t and the fully plastic neutral axis is at the junction of the flange and web since, there, A_c=A_t = 2a². Thus

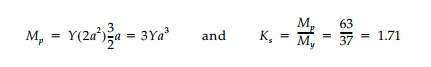
This shape factor is roughly the same for any T beam showing they are even less efficient than rectangular cross-sections in the elastic range.

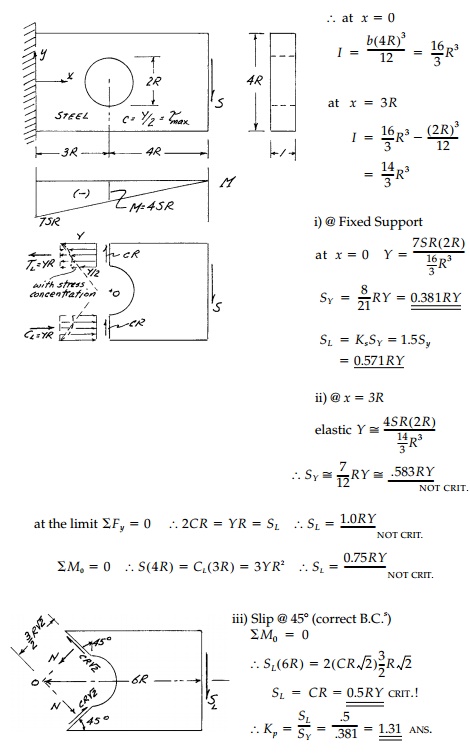
Example 11.1

A steel cantilever beam with a hole in it is loaded with a vertical shear force (distributed parabolically) at its free end as shown. From simple beam theory (plane sections) determine the yield load S_Y . Estimate the limit load from an upper-bound approach and thereby the plasticity factor S_L/S_Y .