Limit Analysis of Frames and Arches

Limit Analysis of Frames and Arches

The upper-bound analysis of frames and arches follows much the same strategy as for beams. However, in addition to the location of enough plastic hinges to bring about collapse, there may be a variety of ways they can be arranged into different “failure mechanisms” and, of course, the interaction effect of axial forces may reduce the moment capacity in a nonlinear way (Figure 11.4) as the loads increase. We will consider a few simple examples to illustrate these concepts.

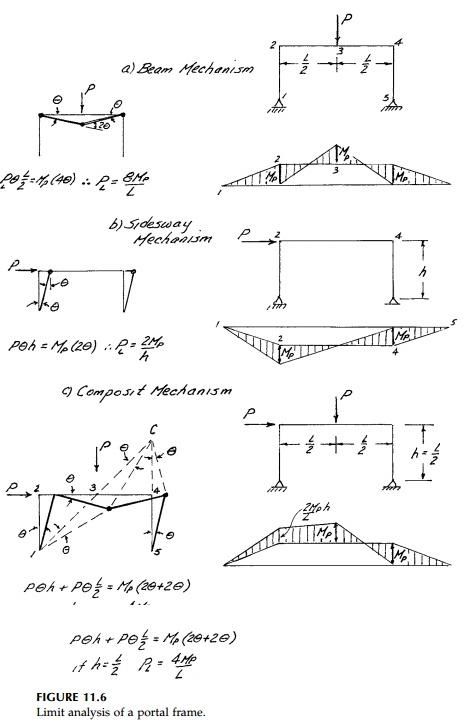
Consider first a basic single-story portal frame (Figure 11.6). For a concen-trated load at midspan, a local beam mechanism would occur at P_L = 8M_P/L. Similarly, if the wind loading is approximated by a concentrated lateral force P at the top, the local “panel” or sidesway mechanism would occur at P_L = 2M_P/h. If, for example, h =L/2 then P_L  = 4M_P/L and the panel mechanism would occur first. Finally, with both loads acting, a composite mechanism is  possible. For the particular case where h = L/2, this mode of collapse occurs simultaneously with the panel mechanism at P_L = 4M_P/L. Also shown in Figure 11.6 is the instantaneous center approach to the virtual work calculation. There are three movable parts that rotate as rigid bodies. Part 123 rotates about 1, part 45 rotates about 5 and part 34 must therefore rotate about a point C, located as shown (since point 3 rotates about both A and C, point 4 rotates about both 5 and C). The instantaneous-center method is particularly useful for gable frames and arches.

Multistory and/or multibay frames are more involved but conceptually no more difficult. An example is presented for a 5-degree indeterminate frame in Figure 11.7. The simplicity of the limit analysis compared to an elastic analysis is dramatic. For an actual design, the moment capacities of the members, par-ticularly the inner columns, would need to allow for the axial-load interaction effects. As might be expected, the critical mechanism has six plastic hinges. As each one forms, the structure becomes one degree less indeterminate until, with the sixth, it becomes unstable giving the extra equilibrium equation needed to solve for the critical load.

The minimization strategy becomes clear as you work with various trial mechanisms. Obviously, you want to reduce the number of hinges and the angles through which they rotate to keep the internal plastic energy low while at the same time getting all the loads to move to increase the external work. Moreover, from a design perspective it quickly becomes apparent where increasing moment capacity can help and where it will not. Since the calculations are so simple so is a design by successive approximation. Usu-ally for structures, determining the collapse load for each possible mecha-nism by equilibrium equations is much more difficult than by using a work calculation. However, when you have found what you think is the upper-bound minimum, in this case P_L = 2M_P/L, you must use the equilibrium equations to solve for the reactions and plot the moment diagram (Figure 11.7d) to make sure that at no point is M> M_P and thereby check that you have, in fact, determined the correct solution.

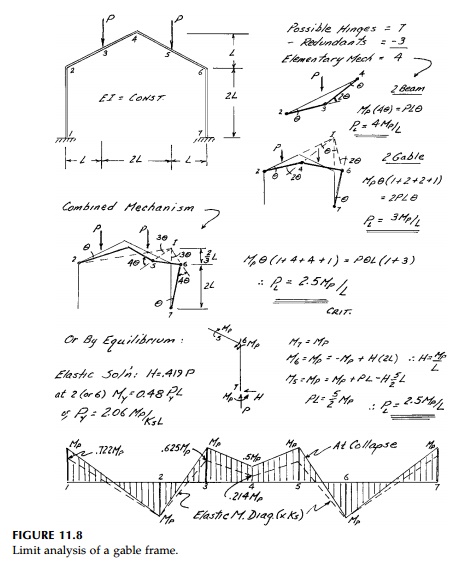
Two further examples of simple limit analysis, a gable frame and a circular arch each with constant cross-section, are shown in Figures 11.8 and 11.9. In both cases the analysis is made easier by assuming concentrated loads. The elastic bending solution is shown for the gable frame to compare to the col-lapse bending moment diagram. The redistribution factor is simply the ratio of the areas of the two.

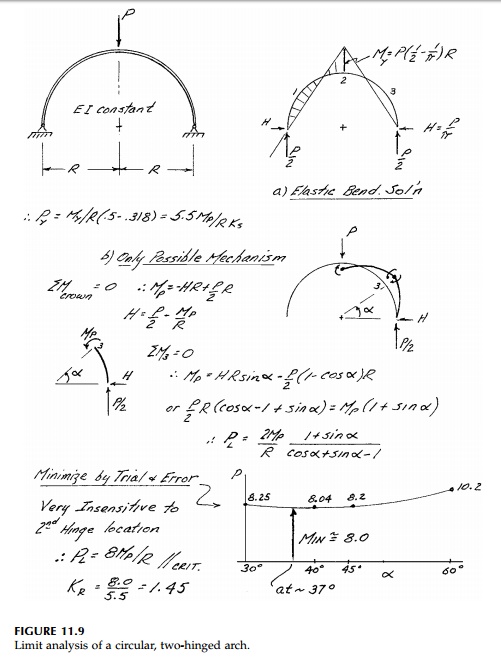
Even with a concentrated load, one possible hinge location is uncertain for the arch and therefore must be determined by application of the upper-bound theorem. A formal equation could be derived, but minimization by trial and error is perfectly adequate. The analysis at these two structures with uniform loads are called for in the chapter problems where determining the critical hinge locations is more difficult. For more complicated structural geometry or loading, graphical analysis for the kinematics of collapse is perfectly adequate and is commonly used in practice. Since real arches are designed to transmit loads primarily by axial force, the bending solution for the collapse load may need to be reduced to include the interaction effect dis-cussed in Section 11.2.