Limit Analysis of Plates

Limit Analysis of Plates

The elastic analysis of plates with a distributed lateral load “q,” while straightforward in concept, can be extremely complicated because of difficul-ties introduced by the boundary conditions. The fundamental governing equation in terms of the lateral deflection, w,

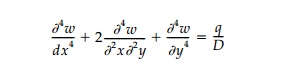
is essentially a “two-way” beam equation where the flexural rigidity of the plate

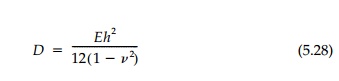
replaces the simple beam rigidity EI. As with a beam, slopes are proportional to the first derivatives, moments to the second derivatives, and shears to the third derivatives of the deflection. Thus the boundary conditions of a free edge, simply-supported edge, and fixed edge can be expressed. In theory, the elastic problem can be solved directly for circular plates, by using Fourier series for rectangular shapes, and by numerical methods for irregular boundaries. Elastic solutions in the form of extensive tables of coefficients are given in the literature for rectangular and circular plates.*

In contrast, the limit analysis of plates using the upper-bound theorem, is straightforward and much easier than elastic analysis. Simply assume a col-lapse mechanism and calculate the corresponding collapse load by the energy balance or by equilibrium. While an elastic analysis may require hours of intensive calculation, a good estimate of the limit load can be determined in a few minutes. Equally important, a good physical feel for the structural behav-ior of the plate is obtained in the process.

Take, for example, the simple case shown in Figure 11.10 of a circular plate of radius, a, and thickness, h, with a uniform vertical load, q, over the entire surface. If the edge is simply supported (free to rotate) the maximum elastic moment at the center is m_{r =} m_t = (3+v)qa²/16. If the edge is built-in (clamped), the moment at the center is reduced to (1+v)qa²/16 while at the edge the radial moment is m_r = - qa²/8 and there is a tangential or twisting moment m_t =  - v qa²/8. The corresponding maximum stresses are, for a sim-ply supported plate:

The plastic analysis follows the procedure developed for linear structures, except that instead of elastic hinge points with a moment capacity M_p = K_s M_y , “hinge” lines develop with a moment capacity per unit length.

Because of the symmetry, the only possible failure mechanism is that, at col-lapse, the surface is pushed downward into a cone as shown in Figure 11.10. The radial hinge lines, along which m_t = m_p, rotate 2ϕ doing internal work while q over the area of a typical differential slice does external work moving downward 4a/3. For simply supported edges, the energy balance gives q_L = 6m_P/a² and a reserve strength from first yield to collapse of K_P  = K_sK_R = 6/3.2 = 1.875. For the case where the edge is fixed, the edge itself of length 2πa becomes a negative hinge line adding ∆W_i = 2πam_pψ to the total internal work. Thus q_L  = 12m_P/a² and the reserve strength q_L/q_Y = K_P = 12/5.33 = 2.25. Thus, not only do plates take greater loads in the elastic range by beam action in two directions rather than one, but they have greater plastic load-carrying capacity than beams for the same reason.

Yield-line limit analysis of plates is the flexural counterpart to yield line or slip-surface analysis for two-dimensional planar structures. Like the punch problem, the determination of the critical yield line can be accomplished by trial and error or by a formal minimization procedure for a particular type of failure mechanism. Only in special cases like circular plates, is the determination of the exact pattern of yield surfaces straightforward. In general, how-ever, for plates of uniform thickness:

i.   Hinge lines are straight with a constant m_P = Yh²/4,

ii.  Axes of rotation are along supports,

iii.  Axes of rotation are over columns , and

iv. Hinge lines pass through axes of rotation of adjacent slab segments.

These rules of thumb, which help guess the critical hinge line patterns, are illustrated with a few examples in Figure 11.11.

As an example of refining the pattern of hinge lines to converge by the upper-bound theorem on the critical limit load, consider a square plate with either pinned or fixed supports shown in Figure 11.12. The elastic solution gives:

The simplest assumption for the failure mechanism is diagonal hinges from the corners shown as pattern #1. The corresponding collapse loads for the simply supported and fixed boundary cases are calculated by equilibrium to illustrate that this approach can be used rather than enforcing the energy balance.

However, the corners of a rectangular plate actually would like to lift off the edge support if not restrained. Thus the moments are negative near the corners, which act as cantilevers. To capture this, a second hinge line pattern (#2 in Figure 11.12) with “corner cantilevers” or “corner levers” should be investigated. For a particular case we see, for the simply supported plate, that by including the diagonal negative hinge at corners, the q_L is reduced by about 2.5%. Minimi-zation by successive trial and error can reduce this further to roughly

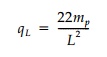
or 9% less than for the simple Pattern #1.

As a final example, consider a 2:1 rectangular plate shown in Figure 11.11. Assuming the simple mechanism without including the corner cantilevers, the limit load works out to be q_L = m_P/7.08 = .1412m_P . Including the corner cantilevers might reduce this 10% to q_L = .127m_P. From the elastic solution

We could now consider what happens if the edges are fixed or if one edge were free, but these and other examples for rectangular plates are left as chap-ter problems.