Plastic “Hinges”

Plastic “Hinges”

Once the cross-section is fully plasticized, it can rotate with no additional moment applied. Thus for a beam subjected to pure moment (with a constant moment diagram), the entire beam plasticizes simultaneously and there is unrestrained plastic flow. In the normal situation where the moment diagram varies, this is not the case.

Consider for example the EPS cantilever beams of rectangular cross-section with a concentrated load, P, at its free end shown in Figure 11.3a. Assume that the cross-section at the wall is on the verge of full plastification 

the stress distribution will be as shown in Figure 11.3d where the elastic zone extends y_e from the neutral axis. Therefore

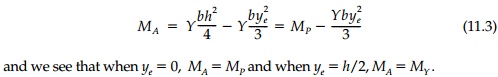
. Since M_A is a known function of x or x* for a given loading, the elastic-plastic interface can be determined from Equation (11.3). In this case,

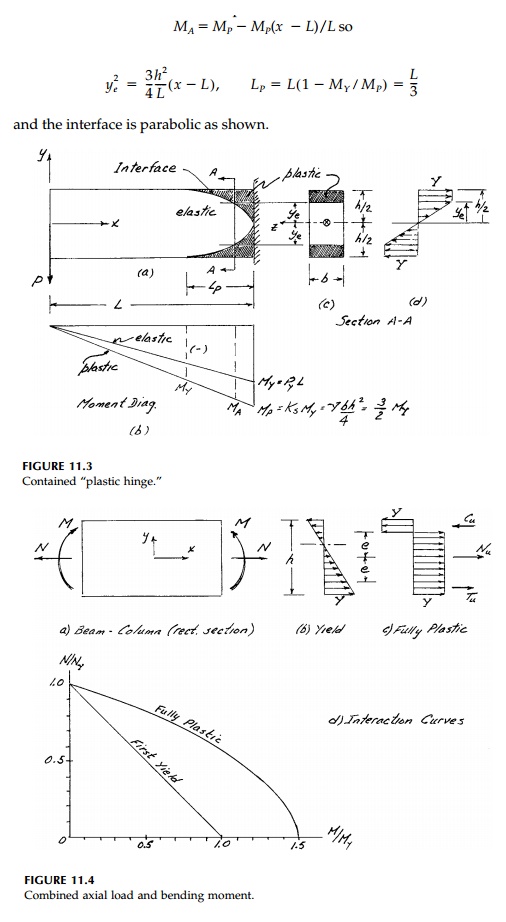
As long as the elastic core remains, plastic flow is constrained. However, when P increases such that PL = M_P , the cross-section becomes fully plastic and the curvature can increase without limit but contained within the plas-tic zone. The beam rotates like a rigid body about a “plastic hinge” holding the ultimate plastic moment M_P . If, as in this case, the structure is determi-nate, it collapses and P_L = M_P/L = K_sM_Y/L. It should be noted that no pro-vision is made in this simple strength-of-materials approach for the effect of any shear stresses, τ_xy , or vertical stress, σ_y , which may be of some signifi-cance in short beams. The chapter problems explore these questions in a preliminary way.

On the other hand, the effect of axial load N combined with bending moment M in the plastic range is straightforward. Suppose N and M combine to give the stress state at yield shown in Figure 11.4b. The maximum stress in the bottom fiber is

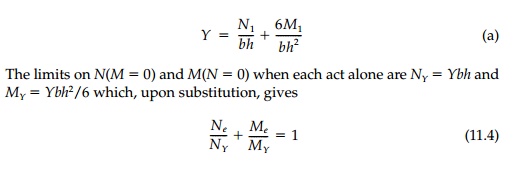
as the elastic interaction curve for yield shown in Figure 11.4d. When N₁ is zero,  M₁ = M_Y and similarly when M₁ = 0, N₁ = N_Y. Between these extremes there are any number of combinations of moment and normal force to cause yield.

If we call N_u and M_u the combination of normal force and moment to fully plasticize the cross-section, it is clear from Figure 11.4c that

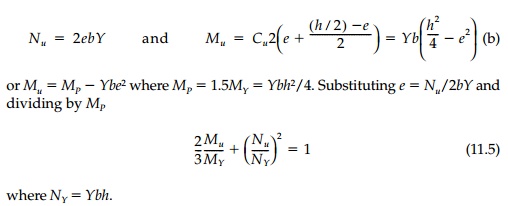
This interaction relationship plotted in Figure 11.4d gives all combinations of N and M for full plastification.