Plastic Torsion

Plastic Torsion

The elastic solution for pure torsion (Previews pages) predicts that the maximum shear stress, τ_zt, is always a maximum on the boundary and is equal to the slope of the pressurized elastic membrane (or ϕ hill) used in Prandtl’s Mem-brane Analogy presented in previews Sections . Using the Prandtl stress function, the shear stresses are

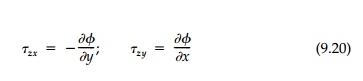
and the equilibrium Equation (9.10) is automatically solved. Now, following the strategy of plasticity, we use the yield condition rather than the compati-bility equation. Writing the Tresca Criterion

Since our boundary condition, ϕ=0, was also based only on equilibrium, it remains applicable in the plastic range. Therefore, the theory of plastic torsion, formulated in terms of Prandtl’s stress function with no reference to strains or displacements, is complete.

Equation (11.8) tells us that the square of the gradient of ϕ, which is the square of the maximum slope of the “ϕ hill” at any point, is equal to the square of the yield stress. Therefore the “ϕ Hill” in regions of the cross-section that have gone plastic have a constant maximum slope equal to τ_Y .

Sand-Hill and Roof Analogies

The solution, that in plastic zones the “ϕ Hill” has a constant maximum slope, suggested to Nadai* in 1923 the so-called sand-heap analogy for full plastification. A slope of dry sand has a natural angle of repose slightly greater than the friction angle which, if exceeded, will cause the particles to roll down the hill. Thus if we take a flat horizontal plate of the same shape as the cross-section under torsion and pour sand on it until it will take no more, the resulting surface satisfies the conditions on the plastic “ϕ Hill” that its maximum slope be constant everywhere and its height be zero at the external boundary. Moreover, the expression for the total torque

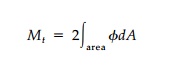
remains valid since it again is based only on equilibrium. Thus the torque applied to the cross-section is twice the volume of sand on the plate (easily determined in the laboratory by weighing it).

We can also think of the sand-hill analogy as a roof of straight sections of constant slope, τ_Y, in the shape of the sand-hill surface erected over the cross-section. This allows us to better visualize stages of partial plastification by thinking of the pressurized membrane inside representing the elastic “ϕ Hill” being pressed flat against the limiting roof in the plastic zones and still curv-ing beneath the roof where the cross-section remains elastic. This is illus-trated in Figure 11.14a for a circular and a square cross-section. At initial yield the membrane first touches the roof at some point or points at the boundary. With further increase in air pressure, which is directly proportional to the rate of twist and therefore the torque, the membrane gradually touches more and more of the roof until, at full plastification, there is no space between them.

These analogies give us both a heuristic way to visualize solutions and, for fairly simple shapes, a device to actually calculate exact values for the fully plastic torque (M_t)_P . Since τ_Y flows along contour lines, it abruptly changes direction at “ridge lines” which, since the slope is constant, must bisect corner angles. Also, since the slope is constant, the contours are equidistant.

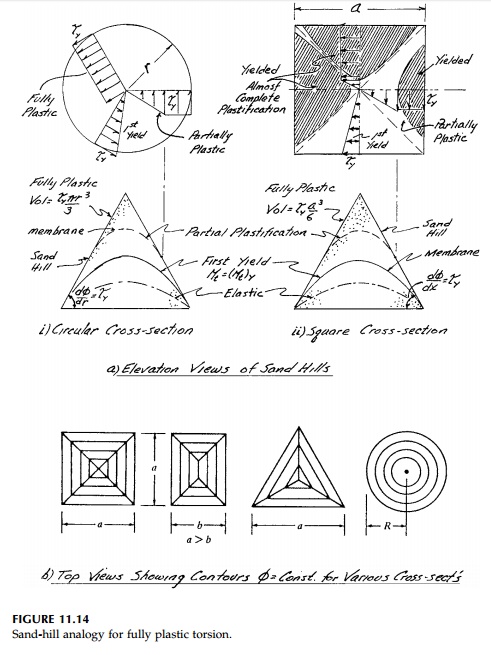
For example, contour lines for some simple shapes are shown in Figure 11.14b. The sand hill for a circular cross-section is a cone of height  τ_YR/2. Thus the ulti-mate torque capacity is:

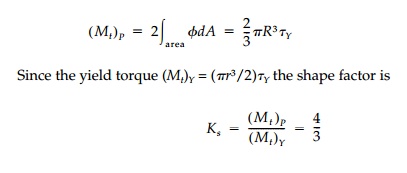
This result for a circular cross-section is, of course, just as easily found by direct integration as is done in the introductory course in strength of materi-als. Calculating the plastic torque and shape factors for a variety of other solid cross-sections including those in Table 9.1 are included as chapter problems. This lower-bound plasticity solution is so straightforward for simple shapes because the sand-hill analogy is so powerful.

Sections with Holes and Keyways

The sand-hill analogy can be applied to sections with holes and keyways, although using it for computation of the plastic torque becomes much more dif-ficult. Consider for example, Figure 11.15b showing a circular hole eccentrically placed in a circular cross-section. We need to visualize that a thin-walled vertical tube is inserted in the hole in the circular plate before the sand is poured on the plate. We then lower the tube allowing the sand to fall down it until its surface area is covered. In Figure 11.15b the top of the tube would be τ_Yh above the plate. Therefore the boundary conditions, θ=0 at the edge of the plate and θ= τ_Yh (constant) on the edge of the hole, are satisfied. Twice the volume of the sand hill is the plastic torque, but it will not be easy to compute.*

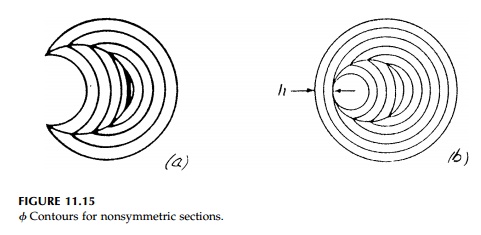
In cases without symmetry such as shown in Figure 11.15, it is easier to draw the contours and compute the plastic torque using the “onion” analogy or “nesting tube” lower-bound approximation presented by Calladine.

We have seen in Section 9.5 (Figure 9.12) from equilibrium considerations only that for thin-walled tubes of arbitrary shape

where A is not the area of the cross-section but the area enclosed by the aver-age perimeter. If we make t a constant, then at yield

Thus we can obtain a lower-bound solution for the plastic torque by dividing the cross-section into a set of nesting thin-walled tubes where each tube has the same constant thickness and encloses the largest possible area.

The procedure is, starting at the outer edge, to cut or strip off complete thin tubes each of the same constant thickness (so τ = τ_Y) until the cross-section is used up. We then sum the torques from each nested tube from Equation (11.9) to give the total plastic torque, which will be a lower bound. Calladine* uses the term “onion” analogy and it is clear that, in the limit, it is the same as the sand-hill analogy. However, it is much clearer conceptu-ally, particularly for complicated shapes, and much easier to draw and compute.

Take, for example, the hollow square tube in Figure 11.16. This strategy of graphical analysis gives a set of nested square tubes. Because of the regular geometry we can reduce the thickness of each tube, 2x on a side, to a differential

This lower-bound approach gives the exact value in this case where calculus can be used.

For cross-sections with holes, the calculation is more difficult but manage-able, and the conceptual visualization is clear. Take for example the circular cross-section with a triangular hole shown in Figure 11.17. Starting from the outside we get four complete nested tubes, but then we are left with three irreg-ular zones. Our striping procedure must produce complete tubes so we con-tinue on as shown. With a ruler, protractor, and some poetic license we can determine the area circumscribed by each of the three onion slices in each of these three areas and their contribution to the total plastic torque. They turn out to be small and neglecting them and using only the four circular tubes gives a satisfactory lower-bound value

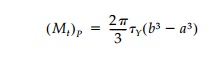
It is clear that this “stripping” procedure is perfectly general and that by using it we can develop a satisfactory lower-bound estimate for the plastic torque for any cross-section, no matter how irregular. Starting from the outside, rings of uniform cross-section are “removed” treating separately any areas that may become separated in the process. Areas can be evaluated by graphical approximations with or without the aid of a planimeter. Figure 11.18 shows

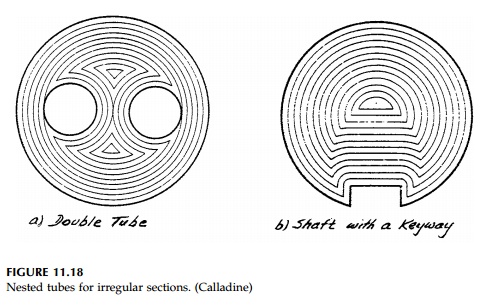
two more examples that emphasize the relative simplicity of the nested-tube approach compared to the sand-hill analogy in visualizing the contours of the “ϕ hill” for complicated sections.