The Bearing Capacity (Indentation) Problem

Example - the Bearing Capacity (Indentation) Problem

The contact problem of a foundation, bearing plate, or punch being driven into a body is encountered throughout engineering practice. As an introduc-tion we will consider here only the simplest idealization by assuming:

1.  The material being indented (the foundation) is an EPS material.

2.  Plane strain (a long indenter) so that the out-of-plane stress is every-where the intermediate principal stress.

3.  The actual distribution of contact pressure is not important and can therefore be considered uniform.

4.  There are no contact shears (a smooth indenter).

5.  The weight of the foundation material can be neglected.

6.  The Tresca yield condition; i.e. 

In succeeding pages a more thorough analysis for this general problem will be given and an “exact” solution obtained for this simple case using slip-line theory. However, it is extremely important to appreciate the simplicity and power of the trial-and-error approach using the upper-bound theorem before it is masked by the complexity of this theory.* For most bearing capacity prob-lems and, for that matter, most two-dimensional problems in general, the assumptions above are only approximate at best and boundary conditions (geometry and loading) are complex. Thus the engineer usually faces problems for which “exact” answers are extremely difficult or impossible to obtain. Good approximate analysis using the upper-bound approach is, however, generally simple and always possible. Moreover, it develops that physical feel and sensi-tivity as to which variables are most significant, which is so essential for good design. Thus the upper-bound concept and its application will be emphasized in this section and hereafter.

Circular Mechanisms

The first and most crucial step in upper-bound analysis is to postulate a geo-metrically possible failure mode or “mechanism” of collapse. The closer this is to the “correct” mechanism, the closer one approaches the “correct” answer, but there are trade-offs involved in that the subsequent calculation of the load to cause collapse must be reasonably easy. In fact, since after the mechanism is selected the problem of evaluating the corresponding failure load is simply a statics problem,* choosing and drawing a collapse mechanism is analogous to selecting the most advantageous free-body diagram to draw in structural analy-sis. Ninety-nine percent of thought and judgment should be spent on this first step since the remaining work is straightforward mechanical application of force equilibrium or its energy counterpart.

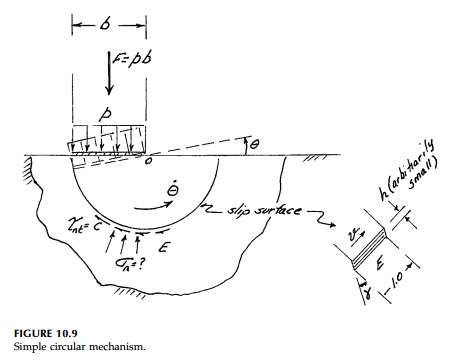
Perhaps the simplest possible mechanism is rotation about one corner as shown in Figure 10.9. The bearing, plate (indenter) rotates as a rigid body with angular velocity ^. around a corner and there is an intense shear zone (a slip surface) outside of which (region E) the EPS foundation material remains elastic. In this zone, which can be made arbitrarily narrow since the plastic plateau is assumed infinite, the shear stress must be

where v velocity of plastic deformation of one surface relative to the other. Therefore, equating external to internal work (in a small time)

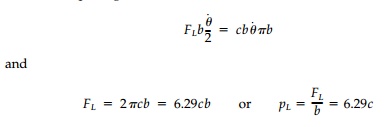
It is important to note that for this circular mechanism, the calculation could just as easily be done using equilibrium by taking moments about the corner at 0:

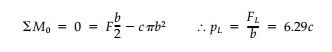
However, this is only possible since the unknown normal stresses on the cir-cular slip surface have no moment arm.

Thus we have found, very simply, an upper-bound estimate for the collapse load and it must be higher than the actual collapse load. The search for pos-sible lower values for circular mechanisms in general can now be pursued by changing the origin and radius. This can be done as in the previous example, either by trial and error using a graphical minimization procedure, or for-mally (see P10.17). However, unlike the example of a loaded beam where the fundamental type of mechanism is known (i.e., plastic hinges), optimization of the location of the circular slip surface to reduce p_L to a minimum will not converge to the exact solution since this type of mechanism (circular) is not the correct shape to start off with (see P10.19).

Sliding Block Mechanisms

Another geometrically possible class of failure modes for this problem is made up of a number of plane, rigid blocks being pushed downward, side-ways, and upward, such as is shown in Figure 10.10. To formulate the energy balance, the relative sliding velocities at each interface must be known.

The velocity (or displacement) diagram shown in Figure 10.10 does this directly.* Each sliding block is designated by a capital letter and the velocity

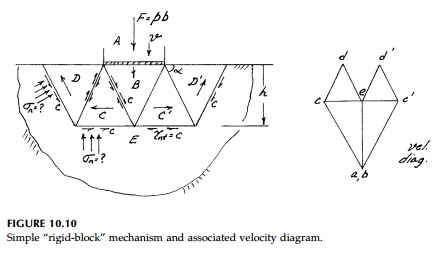
of each block is represented by a single point. Thus the relative velocity between two blocks is that vector joining the two corresponding points.

To construct the diagram, one starts at point e as the zero reference since it represents the stationary elastic portion of the structure. The velocity of the bearing plate (indenter) is laid off to some arbitrary scale (since the magni-tude is unknown). Blocks A and B move vertically the same amount (wedge B is an extension of A) so a and b must coincide. Then C is known since it must be horizontal to e, and at a given angle, to b. Similarly d is located graphically from c and e and the points c' and d' from symmetry.

The energy balance is therefore:

where l is the length of the interface and all energy terms are, of course, posi-tive. Note also that the absolute size of the velocity diagram will have no effect on the calculation. For the mechanism shown, made up of equilateral train gles, all the lengths equal b and

This is 9% less than the simple slip circle mechanism (p_L 6.29c) and it can be reduced slightly by optimizing the size and shape of the triangles (see P10.17). However, this is certainly not the correct family of slip surfaces and thus, no matter how hard we might try to find the optimum layout of rigid sliding blocks in this family of collapse modes, we shall never reach the “exact” value of p_L. As engineers we should not let this bother us too much.

However, for EPS materials and in some cases for more difficult Mohr-Coulomb materials (cast iron, concrete, soil), it is possible to derive from the basic equilibrium equations and yield condition, the geometric characteris-tics of the correct family of ship surfaces. We may even be able to solve for the most critical one and the corresponding exact limit load. This is the topic explored in coming  pages.