Plastic Material Behavior

Concepts of Plasticity

Plastic Material Behavior

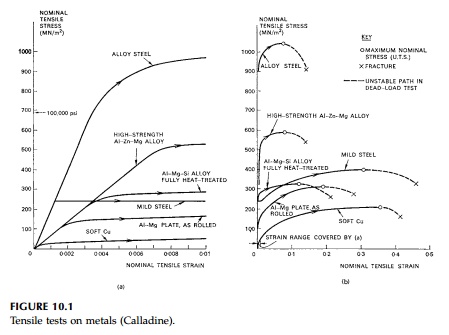
Behavior of a material beyond yield is called its plastic behavior. For this session of pages, we will use the simplest idealization of a perfectly elastic-plastic solid (EPS) with the same yield stress (Y) in tension or compression able to deform at constant Y without strain hardening or strain softening. As can be seen from Figure 10.1, this assumption is not bad for typical metals strained < 1%, but at greater strains most metals exhibit strain hardening. Mild steel is nearly a per-fect EPS below 2% strain.

Since after yield our idealized material offers no further resistance to devia-toric stress, it essentially behaves as a viscous fluid and, without vorticity, must

flow normal to lines of equipotential. For the classical Theory of Plasticity* with an EPS material, the yield function (either Tresca or von Mises) serves as the “plastic potential” hill, F, driving the flow in stress space down its steepest slope, which is the gradient of F. Thus the increments of the total plastic strain or deformation vector, δE_i^p, are found from the partial derivatives.

For the von Mises criterion, for example, where

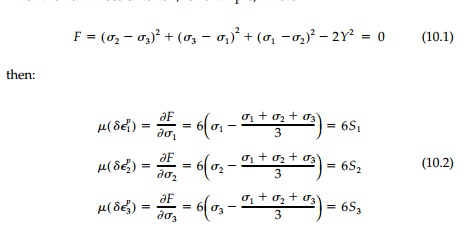
For given values of σ₁,σ₂, σ₃ at yield, these equations fix the relative magnitudes of the plastic strain increments but the scalar, μ, scales their actual values depend-ing on the size of the stress increment (and the slope of the strain-hardening curve; i.e., the plastic work for non-EPS materials).

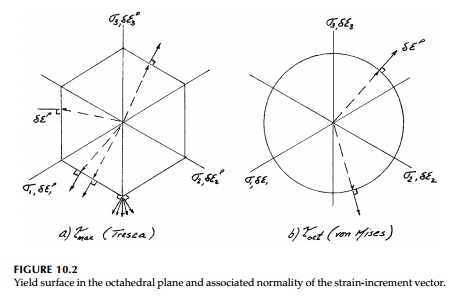
Looking down the stress-space diagonal (the octahedral axis) the yield sur-face is seen in true perspective as an equipotential line and the associated flow rule requires that the total plastic strain increment, δ_EP, be normal to it. This “normality condition” is shown in Figure 10.2 for both criteria. The nor-mality rule is ambiguous only for the Tresca criterion at the six apices of the hexagon, and then only in the 60o range indicated in Figure 10.2. For the von Mises criterion, there is a direct one-to-one correspondence between the direction of the strain increment vector and the deviatoric stress vector and thus the plastic work (the dot product) is a maximum.

Two other important observations can be made:

1.  The plastic strain increment vector does not depend on how we reach the yield surface (the stress path) but only where we are on it. Nor, as simply the gradient of a potential function, does it depend on the stress increment.

2.  Shear flow of an EPS material takes place at constant volume since, from Equation (10.1)

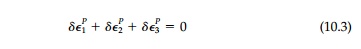
Thus, beyond yield, v^P =1/2 and the material becomes incompressible. Finally it should be noted that this “normality rule” is a more general concept in that it governs not only the plastic flow of EPS materials in stress space, but also applies, as we shall see, to structures made of EPS material when viewed in the appropriate “load space.”