The Lower Bound Theorem

The Lower-Bound Theorem

The load corresponding to any stress distribution throughout the struc-ture, which satisfies equilibrium without violating the yield condition, is a safe estimate of the limit load.

Another way of stating the theorem is:

Of all internal stress distributions that satisfy equilibrium and do not vio-late the yield condition, the collapse (limit) load will be the largest.

When stated the first way, this theorem is sometimes called “the safe theo-rem.” However, the limiting process as we approach the correct solution from below, emphasized in the second version, is the most important concept and therefore the lower-bound name.

The power of this theorem for applications is that we do not need to consider the geometry of deformations but use only stress conditions. There is a straightforward energy proof of the theorem, but the theorem is intuitively sat-isfying since the plasticity equations in Section 10.3 also involve only stress and essentially say the same thing. One important concept, however, which is used in the classic proof for physical understanding is that, in elastic- plastic theory at the collapse load, the stresses throughout do not change as the structure deforms. Thus there are no changes in strain in the “elastic” (or not fully plas-tic) zones during collapse and these regions act essentially as if they were rigid. Basically, the elastic energy is considered insignificant compared to the plastic energy as the individual elements move along the horizontal yield plateau. Similarly for the structure as a whole, the elastic-plastic energy used getting to the limit state can be disregarded in comparison to the fully plastic work as col-lapse progresses. Thus, localized areas of intense shear deformation, called “slip lines,” develop during collapse with the surrounding materials, in com-parison, acting as rigid blocks sliding relative to each other. Since the lower-bound theorem deals with stresses (or forces) and not with deformations (or the failure mechanism), this important concept, although used in the proof, is not needed in the application of the lower-bound approach. However, it becomes the crucial consideration in upper-bound analysis treated in the next section, which in turn, becomes the main focus of succeeding chapters.

To return to our example of a thick ring in plane stress under internal pres-sure, let us pretend we do not know the answer and approach the limit state by applying the lower-bound theorem. We, therefore, seek a stress distribu-tion satisfying the equilibrium equation (on a differential scale):

Cutting the ring through any diameter gives another overall equilibrium rela-tionship in terms of stress resultants:

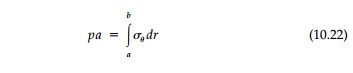
Clearly any number of possible stress distributions are possible. Our choice is wide open because any distribution of σ_r that satisfies the boundary conditions [Equation (10.20)] may be substituted into Equation (10.2) to give the corresponding (σθ) and then p_L determined so that Equation (10.21) is not violated.

An obvious and simple choice is a linear distribution as shown in Figure 10.7. For the ring with b   2a:

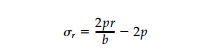
which satisfies the boundary conditions [Equation (10.20)]. Substituting into Equation (10.2):

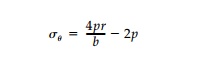
which is also linear and has a maximum value of 2p at r b. Equation (10.22) is satisfied and since the yield criterion must not be violated anywhere

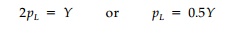
This, as we know, is 28% lower than the correct value of 0.693Y, but 33% higher than first yield.

Obviously to come closer to the exact value we must guess a distribution of σ_r and thereby  σθ that come closer to the yield condition throughout the cross-section. There are obviously better strategies for making educated guesses. One method is to specify σθ(r) and determine  σr(r) from the equilibrium equa-tion rather than the other way around. The elastic solution is a very useful clue as to how to proceed, but the lower-bound approach is in no way dependent on knowing the elastic solution beforehand.