The Upper Bound Theorem

The Upper Bound Theorem

If an estimate of the collapse load of a structure is made by equating in-ternal rate of dissipation of energy to the rate external forces do work for any postulated mechanism of deformation (collapse mechanism), the esti-mate will either be high or correct.

This version of the upper-bound theorem emphasizes the important con-cept for its application of first guessing a failure mechanism. It also implies the importance of considering the plastic deformations associated with this collapse mechanism. Another way of stating the theorem is: Of all methods of collapse, the actual failure mechanism will require the least amount of force (or energy). This version couches the fundamental idea in terms of minimizing force. Either statement stipulates that we approach the correct solution from above not, as for the lower-bound theorem, from below.

Again this theorem is intuitively obvious and really needs no proof. We would expect, by definition, that a structure would naturally “choose to” col-lapse at the lowest possible load and if this were not the case, something would be wrong with the world.

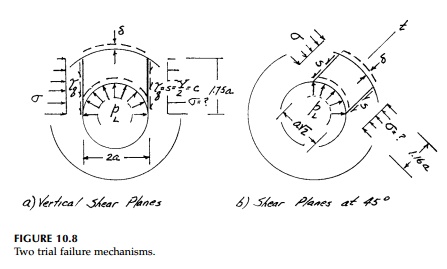
To return to our example of a thick ring (b 2a), the failure mechanism seems to be tensile yielding across a cross-section. However, since shear causes plastic flow, we would expect from the elastic solution that yield would develop at 45^o to the r - θ orientation of principal stresses. For illustration, however, let us first guess the failure mechanism shown in Figure 10.8a. Along the shear surface, the shear stress is known to be the shear strength

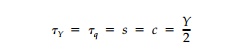
but the normal stress is unknown. However, because we have anticipated this difficulty and chosen a failure mechanism with parallel slip surfaces, we

can sum forces in this direction and the normal stresses on the failure planes do not enter into the equilibrium equation.* Equating vertical forces:

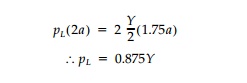
The length of the shearing surface, 1.75a, was scaled from the drawing rather than calculated exactly.

Similarly, for a second set of parallel slip planes at 45^o to the vertical (Figure 10.8b).

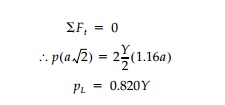
where again the slip length, 1.16a, is measured rather than computed. Note that rather than use an energy calculation, the limit load was obtained directly from equilibrium. Often this is easier and simpler to visualize but either a vir-tual work or an equilibrium calculation is equally valid.

As might be expected, the second choice of failure mechanism is somewhat better than the first (giving a lower estimate for p_L) since it at least starts off from the inner boundary in the correct orientation of 45^o. Neither is very good, however.