Plasticity Field Equations and Thick Ring

Plasticity Field Equations

Equilibrium must apply whether the material is behaving elastically or plas-tically or whatever. Moreover, in the plastic zone and normal and tangential to the elastic-plastic interface, the shear stress must equal the shear strength. In the surrounding elastic regions (Figure 10.4) where the stress�' strain relationship is still linear, the geometric compatibility requirement in terms of stresses still applies. Thus the field equations in terms of stress

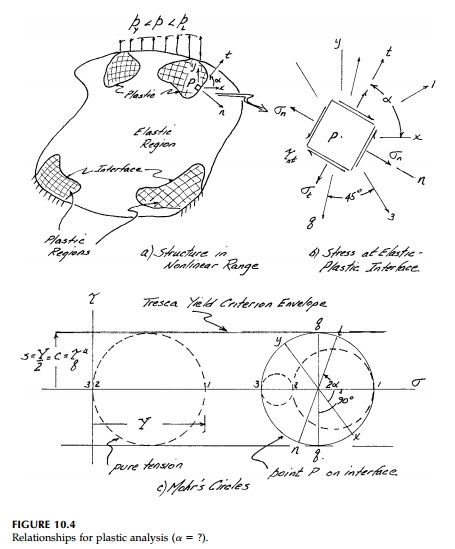
In theory, then, there is enough information (3 equations, 3 unknowns) to solve the field problem if the shape and extent of the plastic zones can be deter-mined as they develop.* In practice this is very difficult except for special cases with extreme symmetry and/or conditions which greatly simplify the equa-tions.

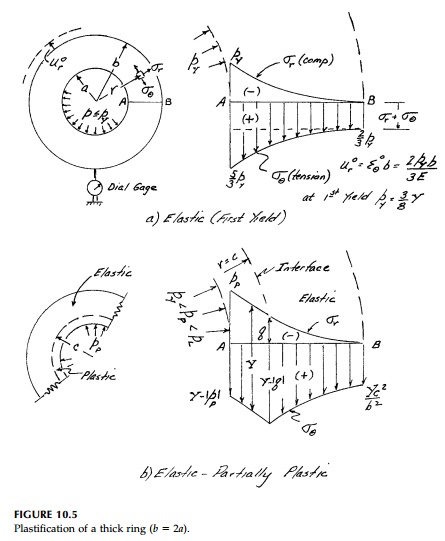
Example-Thick Ring

One such special case where the full plasticity behavior can be found from first yield to collapse is a thick ring (Figure 10.5). There is only one meaning-ful equilibrium equation:

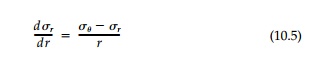
since there is no change in the field with respect to . From symmetry the in-plane displacements are:

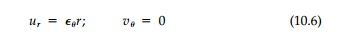
and these conditions apply throughout the elastic and plastic range. The elas-tic stress field for internal pressure only is, from Section 6.5:

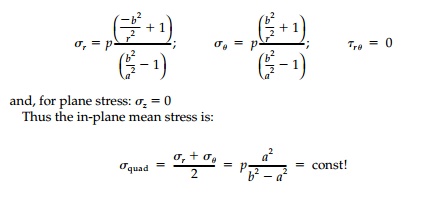
and the state of stress at any point is simply a state of pure shear superim-posed on “hydrostatic tension.” Since for plane stress,  σθ < σz < σ_r the yield

Although the ring yields at this pressure, it will not fail. As the pressure increases, the yield interface moves outward radially and, as the plastic zone enlarges, the stresses must adjust to provide equilibrium while satisfying the boundary conditions that at

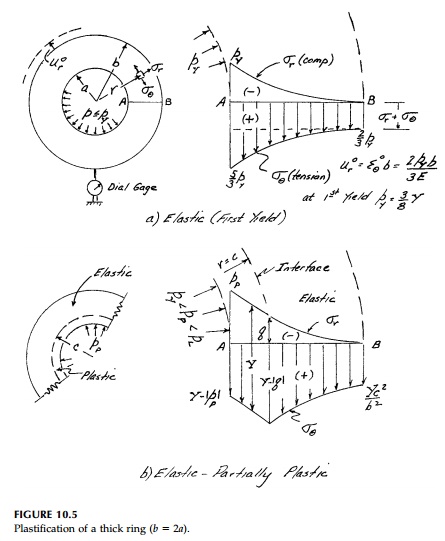
Figure 10.5b shows such a state where the elasticity solution still applies at r>= c. At the interface, r c, the outer “ring,” which is still elastic, cannot tell the differ-ence between the radial stress or an equivalent pressure, q, where

Thus, if a factor of safety of 1.5 was specified to determine the “allowable” pressure against yield (i.e., the “working stress”)

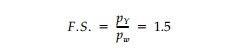
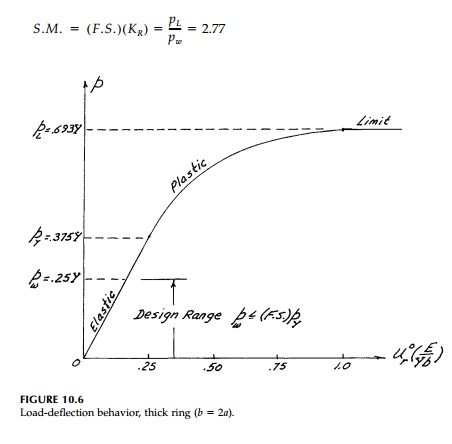
there would actually be a total safety margin* of

The elastic-plastic radial deformation of the outer circumference can be found directly since it remains elastic until the limit state is reached. At r - b with c sub-stituted for a and q for p in Equation (10.4)

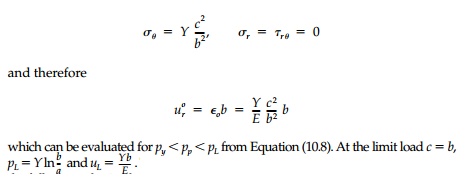
The load-deformation curve shown in Figure 10.6 illustrates the full-range, elastic-plastic behavior of a ring with b  = 2a made of EPS material.