Percentage and Simple Interest

Chapter 2

PERCENTAGE AND SIMPLE INTEREST

Learning Objectives

● To understand the meaning of per cent.

● To convert a fraction into percentage and vice-versa.

● To convert a decimal number into percentage and vice-versa.

● To solve problems on percentage.

● To find simple interest by formula.

● To apply simple interest formula in different situations.

Introduction

We have already been introduced to the concepts such as ‘Ratio and proportion’, unitary method and its use in solving day-to-day application problems. Also, ratio has been explained as a method of comparison by division. One of the most common methods to compare two quantities is by using percentage.

Solution

Geetha scored 475 marks out of 600 and Seetha scored 425 out of 500. Can we conclude Geetha has scored higher marks than Seetha? Is it right? Whom do you think has done better?

We cannot decide who has done better by just comparing the marks, they have scored because the maximum marks in both the cases are different.

To get an answer for these situations, we use “Percentage”. We are going to see about “percentage” in this chapter.

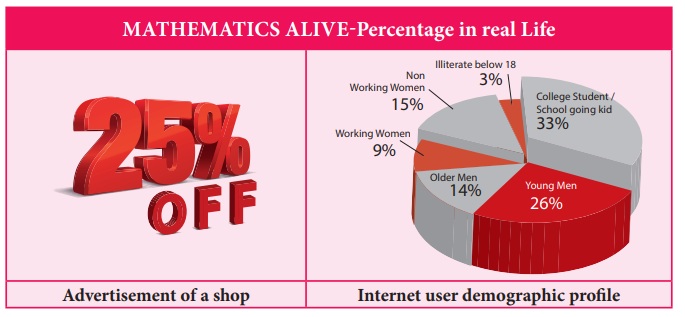
MATHEMATICS ALIVE-Percentage in real Life

Per cent is derived from the Latin word ‘Per centum’ meaning ‘per hundred’. Per cent is denoted by the symbol ‘%’ and means hundredth too. That is 1% means 1 out of hundred or one hundredth which can be written as 1% = 1/100 = 0 .01. It is read as 1 per cent.

In the same way, 50% means 50 out of hundred or fifty hundredth. That is 50% = 50/100

 80% means 80 out of hundred or eighty hundredth. That is 80% = 80/100

20% means 20 out of hundred or twenty hundredth. That is 20% = 20/100

To understand this let us do the following activity.

Activity

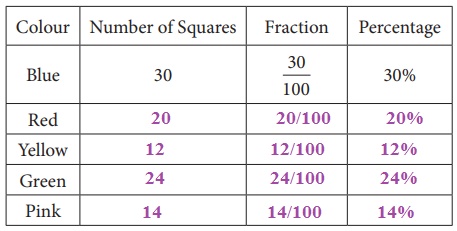
Take a 10 × 10 square grid to recall the previous knowledge on fraction. The grid is shaded using 5 different colours. The particulars related to blue colour shaded portion shown in the grid is given in the table below. Observe the grid and complete the table.

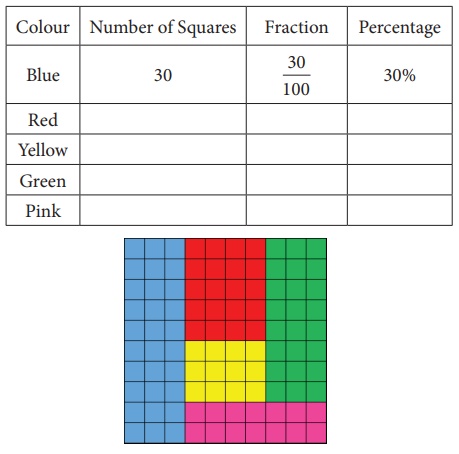
From this we can understand that percentage can be written as a fraction with denominator hundred.

Try these

Find the percentage of children whose scores fall in different categories given in table below.

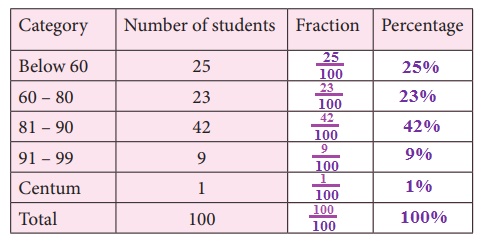
In all these examples, the total number of items add upto 100. Can we calculate those percentage of items if the total number do not add upto 100? Yes. We can find the percentage of items. In such cases we need to convert the given fractions to their equivalent fraction with denominator 100.

For example consider a 5 × 10 square grid.

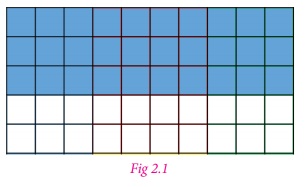
In the Fig 2.1, the blue shaded portion of the grid represents the fraction 30/50. Which is equal to 60/100 or 0.60 or 0.6 or 60%.

Try these

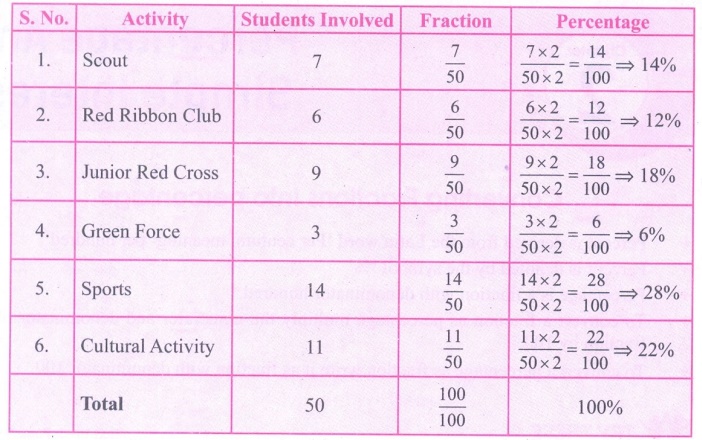
There are 50 students in class VII of a school. The number of students involved in these activities are :

Scout – 7 Red Ribbon Club – 6 Junior Red Cross – 9 Green Force – 3 Sports – 14 Cultural activity – 11

Find the percentage of students who involved in various activities.

Solution: