Percentage in Real Life

Percentage in Real Life

We have seen how percentage are used in comparison of quantities. We also learnt to convert fractions and decimals to percentage and vice-versa.

Now we shall see some situations that use percentage in real life such as 5% of income is allotted for saving; 20% of children’s picture book is coloured green; a book distributor gets 10% of profit on every book sold by him. What can we conclude from these situations.

Percentage as a value

Example 2.14

 There are 50 students in a class. If 14% are absent on a particular day, find the number of students present in the class.

Solution:

Number of students absent on a particular day = 14 % of 50

                                                                           = 14/100 ×50= 7

Therefore, the number of students present = 50 − 7 = 43 students.

Example 2.15

Kuralmathi bought a raincoat and saved ₹ 25 with discount of 20%. What was the original price of the raincoat?

Solution:

Let the price of the raincoat (in ₹ ) be P. So 20% of P = 25

                                                                 (20/100) × P = 25

                                                          P = (25 ×100) /20 = 125

Therefore, the original price of the raincoat is ₹ 125.

Example 2.16

An alloy contains 26 % of copper. What quantity of alloy is required to get 260 g of copper ?

Solution:

Let the quantity of alloy required be Q g

Then 26 % of Q =260 g

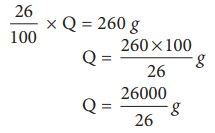
[26/100] × Q = 260 g

260/100  ×  Q = 260 g

 Q = (260 × 100) / 26 g

Q = 26000 / 26 g

Q = 1000 g

Therefore, the required quantity of alloy is 1000 g.

Ratios as percentage

Sometimes ingredients used to prepare food can be represented in the form of ratio. Let us see some examples.

Example 2.17

Kuzhal’s mother makes dosa by mixing the batter made from 1 portion of Urad dhal with 4 portions of rice. Represent each of the ingredients used in the batter as percentage.

Solution:

Representing ingredients used in the batter as ratio, we get, rice : urad dhall = 4 : 1

Now, the total number of parts is 4 + 1 = 5 .

That is, 4/5 portion of rice is mixed with 1/5 portion of urad dhall.

 Thus, the percentage of rice would be   4/5 ×100% = 400/5 %= 80%

The percentage of urad dhall would be 1/50 ×100% = 100/5 %= 20%

Example 2.18

A family cleans a house for pongal celebration by dividing the work in the ratio 1:2:3. Express each portion of work as percentage.

Solution:

The total number of parts of the work is 1 + 2 + 3 = 6

That is, the work is divided into 3 portions as 1//6,2/6 and 3/6.

 Thus, the percentage of 1/6 ^th portion of work would be 1/6 ×100% = 100/6 %=16 (2/3) %

 Similarly, the percentage of 2/6 ^th portion of work would be 1/2 × 100% = 200/6 %= 33 (1/3) %

 Similarly, the percentage of 3/6 th portion of work would be 3/6 × 100% = 300/6 % = 50%

Increase or decrease as Percentage

There are situations where we need to know the increase or decrease of a certain quantity as percentage. Let us see few examples.

Example 2.19

During Aadi sale the price of shirt decreased from ₹ 90 to ₹ 50. What is the percentage of decrease.

Solution:

Original price = the price of the shirt before Aadi month

Amount of change = the decrease in the price = 90 – 50 = ₹ 40

Therefore, the percentage of decrease = [ Amount of change / Original amount ] ×100

                                                             = 40/90 ×100 = 400/9

                                                              = 44 (4/9) %

Example 2.20

The number of literate persons in a city increased from 5 lakhs to 8 lakhs in 5 years. What is the percentage of increase?

Solution:

Original amount = the number of literate persons initially = 5 lakhs

Amount of change = increase in the number of literate persons = 8 – 5 = 3 lakhs

Therefore, the percentage of increase  = ( Amount of change/ Original amount )  ×100

                                                            = 3/5 ×100 = 60%

Try these

Level of water in a tank is increased from 35 litres to 50 litres in 2 minutes, what is the percentage of increase?

Profit or Loss as a Percentage

We have learnt already profit and loss of items. Now we will see how a profit or loss can be converted to percentage. That is, to find the profit % or loss %, we will see some examples.

Example 2.21

A shopkeeper bought a chair for ₹ 325 and sold it for ₹ 350. Find the profit percentage.

Solution:

 Profit per cent  = ( Profit / C.P ) ×100

 = (25/325) × 100 = 100/13 = 7 (9/13) %.

Example 2.22

A T-shirt bought for ₹ 110 is sold at ₹ 90. Find the loss percentage.

Solution:

Cost price of T-shirt is ₹ 110 and Selling price is ₹ 90. So, the loss is ₹ 20

Hence, for ₹ 100 the loss is 20/110 ×100 = 200×11 = 18 (2/11)% .

Example 2.23

 An item was sold at ₹ 200 at a loss of 4 %. What is its cost price.

Solution:

To find the cost price,

Loss per cent = [ Loss / C.P ] ×100

4% = [ Loss / C.P ] ×100

4% = Loss/200 ×100

Loss = 8

C.P = S.P + Loss

      = 200+8

      = 208

Hence the cost price of the item is ₹ 208.

The world's population is growing by 1.10 % per year.

50.4 % of the world's population is male and 49.6 % is female.