Partition Measures

Partition Measures

Quartiles

There are three quartiles denoted by Q₁, Q₂ and Q₃ divides the frequency distribution in to four equal parts

That is 25 percent of data will lie below Q₁, 50 percent of data below Q₂ and 75 percent below Q₃. Here Q₂ is called the Median. Quartiles are obtained in almost the same way as median

Quartiles for Raw or Ungrouped data:

If the data set consist of n items and arranged in ascending order then

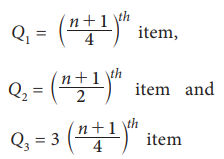
Example 5.30

Compute Q₁ and Q₃ for the data relating to the marks of 8 students in an examination given below 25, 48, 32, 52, 21, 64, 29, 57 

Solution:

  n = 8

 Arrange the values in ascending order

 21, 25, 29, 32, 48, 52, 57, 64 we have

Quartiles for Discrete Series (grouped data)

Step 1: Find cumulative frequencies

Step 2 : Find ((N+1)/ 4)

Step 3 : See in the cumulative frequencies, the value just greater than ((N+1)/ 4) the corresponding value of x is Q₁

Step 4 : Find 3((N+1)/ 4)

Step 5 : See in the cumulative frequencies, the value just greater than 3((N+1)/ 4) then the corresponding value of x is Q3.

Example 5.31

Compute Q₁ and Q₃ for the data relating to age in years of 543 members in a village

Solution:

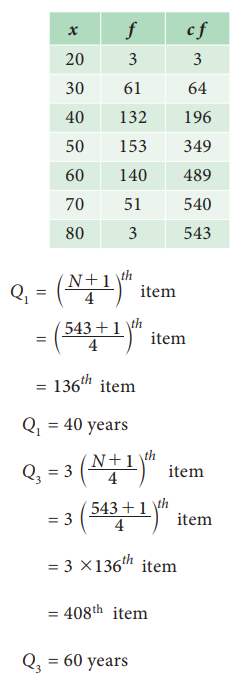
Quartiles for Continuous series (grouped data)

Step 1: Find cumulative frequencies

Step 2 : Find (N/4)

Step 3 : Q₁ class is the class interval corresponding to the value of the cumulative frequency just greater than (N/4)

Step 4 : Q3 class is the class interval corresponding to the value of the cumulative frequency just greater than 3 (N/4)

Example 5.32

Calculate the quartiles Q₁ and Q₃ for wages of the labours given below

Solution:

Deciles

Deciles are similar to quartiles. Quartiles divides ungrouped data into four quarters and Deciles divide data into 10 equal parts .

Example 5.33

Find the D₆ for the following data 

11, 25, 20, 15, 24, 28, 19, 21

Solution:

Arrange in an ascending order

11,15,19,20,21,24,25,28

Example 5.34

Calculate D₅ for the frequency distribution of monthly income of workers in a factory

Solution:

Percentiles

The percentile values divide the frequency distribution into 100 parts each containing 1 percent of the cases. It is clear from the definition of quartiles, deciles and percentiles

Relationship

 P₂₅ = Q₁

 P₅₀ = Median = Q₂

 P₇₅ = 3rd quartile = Q₃

Example 5.35

The following is the monthly income (in 1000) of 8 persons working in a factory. Find P₃₀ income value

10,14, 36, 25, 15, 21, 29, 17

Solutions:

Arrange the data in an ascending order.

 n = 8

 10,14,15,17,21,25,29,36

Example 5.36

Calculate P₆₁ for the following data relating to the height of the plants in a garden

Solution: