Mode

Mode

According to Croxton and Cowden, ‘The mode of a distribution is the value at the point around which the items tend to be most heavily concentrated.

In a busy road, where we take a survey on the vehicle - traffic on the road at a place at a particular period of time, we observe the number of two wheelers is more than cars, buses and other vehicles. Because of the higher frequency, we say that the modal value of this survey is ‘two wheelers’

Mode is defined as the value which occurs most frequently in a data set. The mode obtained may be two or more in frequency distribution.

Computation of mode:

(a) For Ungrouped or Raw Data:

The mode is defined as the value which occurs frequently in a data set

Example 5.21

The following are the marks scored by 20 students in the class. Find the mode 90, 70, 50, 30, 40, 86, 65, 73, 68, 90, 90, 10, 73, 25, 35, 88, 67, 80, 74, 46

Solution:

Since the marks 90 occurs the maximum number of times, three times compared with the other numbers, mode is 90.

Example 5.22

A doctor who checked 9 patients’ sugar level is given below. Find the mode value of the sugar levels. 80, 112, 110, 115, 124, 130, 100, 90, 150, 180

Solution:

Since each values occurs only once, there is no mode.

Example 5.23

Compute mode value for the following observations.

2, 7, 10, 12, 10, 19, 2, 11, 3, 12

Solution:

Here, the observations 10 and 12 occurs twice in the data set, the modes are 10 and 12.

For discrete frequency distribution, mode is the value of the variable corresponding to the maximum frequency.

Example 5.24

Calculate the mode from the following data

Solution:

Here, 7 is the maximum frequency, hence the value of x corresponding to 7 is 8.

Therefore 8 is the mode.

(b) Mode for Continuous data:

The mode or modal value of the distribution is that value of the variate for which the frequency is maximum. It is the value around which the items or observations tend to be most heavily concentrated. The mode is computed by the formula.

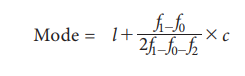
Modal class is the class which has maximum frequency.

f1 = frequency of the modal class

f0 = frequency of the class preceding the modal class

f2 = frequency of the class succeeding the modal class

c = width of the class limits

Example 5.25

The following data relates to the daily income of families in an urban area. Find the modal income of the families.

Solution:

Determination of Modal class:

For a frequency distribution modal class corresponds to the class with maximum frequency. But in any one of the following cases that is not easily possible.

i. If the maximum frequency is repeated.

ii. If the maximum frequency occurs in the beginning or at the end of the distribution

iii. If there are irregularities in the distribution, the modal class is determined by the method of grouping.

Steps for preparing Analysis table:

We prepare a grouping table with 6 columns

i.               In column I, we write down the given frequencies.

ii.               Column II is obtained by combining the frequencies two by two.

iii.               Leave the Ist frequency and combine the remaining frequencies two by two and write in column III

iv.               Column IV is obtained by combining the frequencies three by three.

v.               Leave the Ist frequency and combine the remaining frequencies three by three and write in column V

vi.               Leave the Ist and 2nd frequencies and combine the remaining frequencies three by three and write in column VI

Mark the highest frequency in each column. Then form an analysis table to find the modal class. After finding the modal class use the formula to calculate the modal value.

Example 5.26

Calculate mode for the following frequency distribution:

Solution:

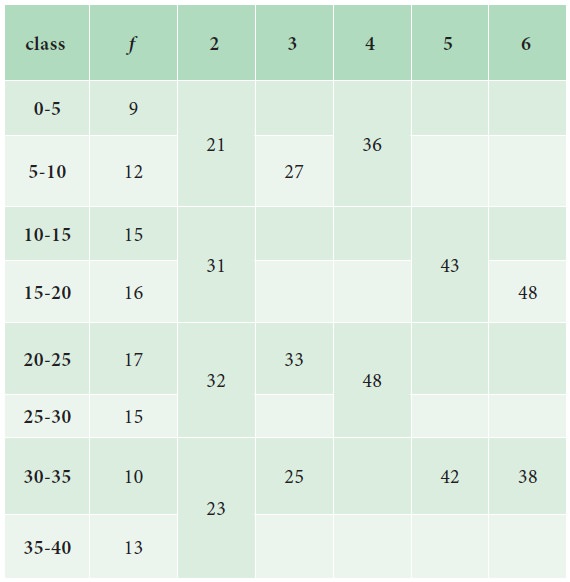
Analysis Table:

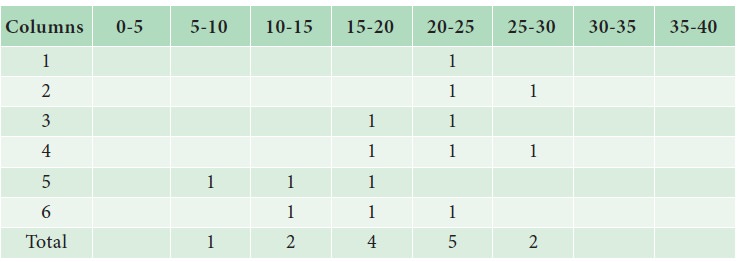
 The maximum occurred corresponding to 20-25, and hence it is the modal class.

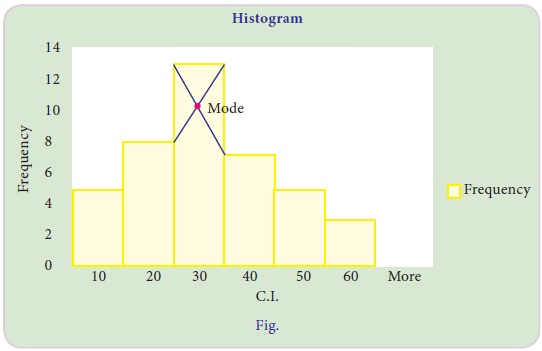
(c)  Graphical Location of Mode

The following are the steps to locate mode by graph

i.               Draw a histogram of the given distribution.

ii.               Join the rectangle corner of the highest rectangle (modal class rectangle) by a straight line to the top right corner of the preceding rectangle. Similarly the top left corner of the highest rectangle is joined to the top left corner of the rectangle on the right.

iii.               From the point of intersection of these two diagonal lines, draw a perpendicular line to the x –axis which meets at M.

iv.               The value of x coordinate of M is the mode.

Example 5.27

Locate the modal value graphically for the following frequency distribution

Solution:

Merits of Mode:

·           It is comparatively easy to understand.

·           It can be found graphically.

·           It is easy to locate in some cases by inspection.

·           It is not affected by extreme values.

·           It is the simplest descriptive measure of average.

Demerits of Mode:

·           It is not suitable for further mathematical treatment.

·           It is an unstable measure as it is affected more by sampling fluctuations.

·           Mode for the series with unequal class intervals cannot be calculated.

·           In a bimodal distribution, there are two modal classes and it is difficult to determine the values of the mode.

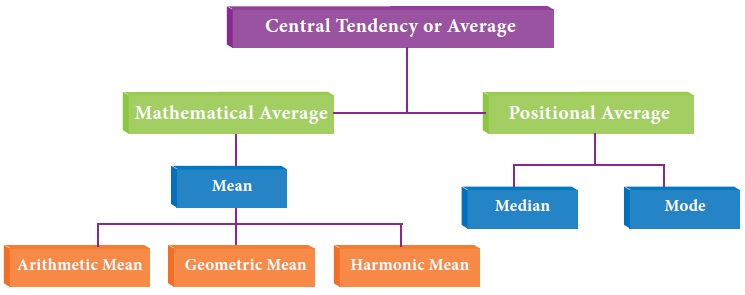
Various measures of central tendency