Harmonic Mean (H.M.)

Harmonic Mean (H.M.)

Harmonic Mean is defined as the reciprocal of the arithmetic mean of reciprocals of the observations.

(a) H.M. for Ungrouped data

Let  x1, x2, ..., xn be the n observations then the harmonic mean is defined as

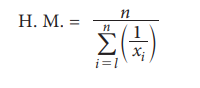
Example 5.11

A man travels from Jaipur to Agra by a car and takes 4 hours to cover the whole distance. In the first hour he travels at a speed of 50 km/hr, in the second hour his speed is 64 km/hr, in third hour his speed is 80 km/hr and in the fourth hour he travels at the speed of 55 km/hr. Find the average speed of the motorist.

Solution:

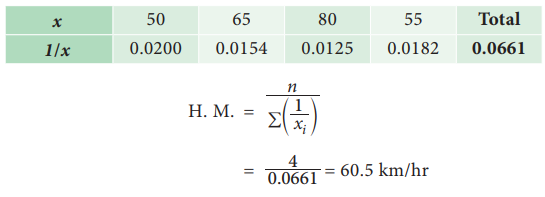
Average speed of the motorist is 60.5km/hr

(b) H.M. for Discrete Grouped data:

For a frequency distribution

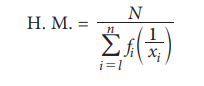
Example 5.12

The following data is obtained from the survey. Compute H.M

Solution:

(c) H.M. for Continuous data:

Where xi is the mid-point of the class interval

Example 5.13

Find the harmonic mean of the following distribution of data

Solution:

Merits of H.M:

·           It is rigidly defined

·           It is based on all the observations of the series

·           It is suitable in case of series having wide dispersion

·           It is suitable for further mathematical treatment

·           It gives less weight to large items and more weight to small items

Limitations of H.M:

·           It is difficult to calculate and is not understandable

·           All the values must be available for computation

·           It is not popular due to its complex calculation.

·           It is usually a value which does not exist in series

When to use?

Harmonic mean is used to calculate the average value when the values are expressed as value/unit. Since the speed is expressed as km/hour, harmonic mean is used for the calculation of average speed.

Relationship among the averages:

In any distribution when the original items are different the A.M., G.M. and H.M would also differ and will be in the following order:

A.M. ≥ G.M ≥ H.M