Geometric Mean(GM)

Geometric Mean(GM)

(a) G.M. For Ungrouped data

The Geometric Mean (G.M.) of a set of n observations is the nth root of their product. If x1, x2, ... , xn are n observations then

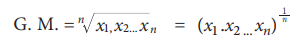
Taking the nth root of a number is difficult. Thus, the computation is done as under

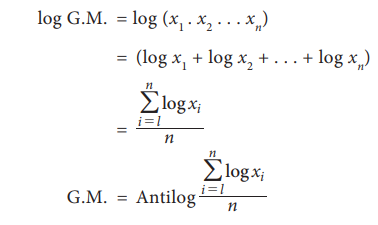
Example 5.7

Calculate the geometric mean of the annual percentage growth rate of profits in business corporate from the year 2000 to 2005 is given below

50, 72, 54, 82, 93

Solution:

Geometrical mean of annual percentage growth rate of profits is 68.26

Example 5.8

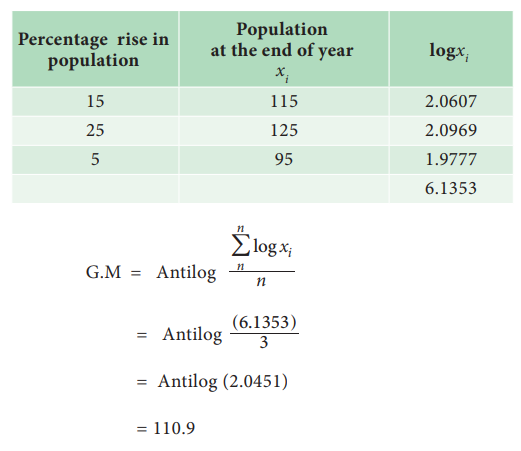
The population in a city increased at the rate of 15% and 25% for two successive years. In the next year it decreased at the rate of 5%. Find the average rate of growt

Solution:

Let us assume that the population is 100

(b) G.M. For Discrete grouped data

If x1, x2,……xn are discrete values of the variate x with corresponding frequencies f1, f2, ... fn. Then geometric mean is defined as

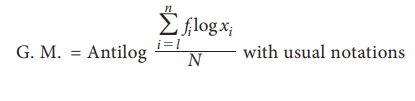
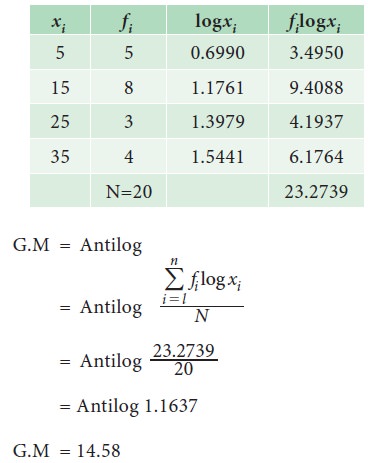
Example 5.9

Find the G.M for the following data, which gives the defective screws obtained in a factory.

Solution:

(c) G.M. for Continuous grouped data

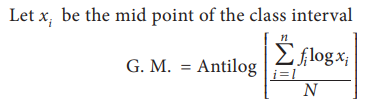
Example 5.10

The following is the distribution of marks obtained by 109 students in a subject in an institution. Find the Geometric mean.

Solution:

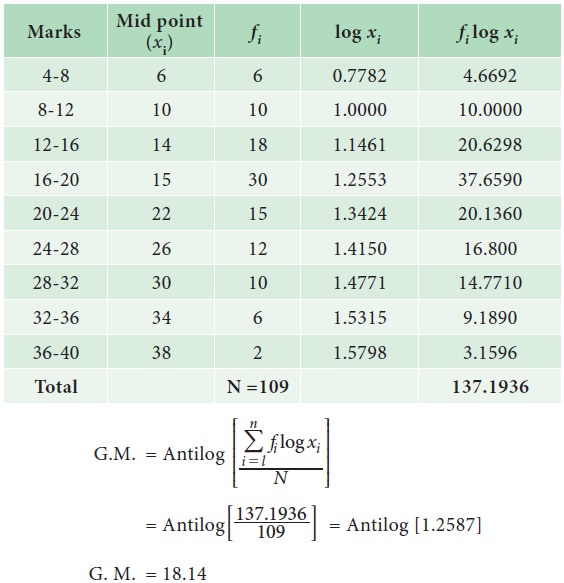
Geometric mean marks of 109 students in a subject is 18.14

Merits of Geometric Mean:

·           It is based on all the observations

·           It is rigidly defined

·           It is capable of further algebraic treatment

·           It is less affected by the extreme values

·           It is suitable for averaging ratios, percentages and rates.

Limitations of Geometric Mean:

·           It is difficult to understand

·           The geometric mean cannot be computed if any item in the series is negative or zero.

·           The GM may not be the actual value of the series

·           It brings out the property of the ratio of the change and not the absolute difference of change as the case in arithmetic mean.