Formula, Solved Example Problems - Arithmetic Mean | 11th Statistics : Chapter 5 : Measures of Central Tendency
Chapter: 11th Statistics : Chapter 5 : Measures of Central Tendency
Arithmetic Mean
Arithmetic Mean
(a) To find A.M. for Raw data
For a raw data, the arithmetic mean of a series of numbers is sum of all observations divided by the number of observations in the series. Thus if x1, x2, ..., xn represent the values of n observations, then arithmetic mean (A.M.) for n observations is: (direct method)
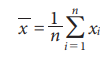
There are two methods for computing the A.M :
(i) Direct method
(ii) Short cut method.
Example 5.1
The following data represent the number of books issued in a school library on selected from 7 different days 7, 9, 12, 15, 5, 4, 11 find the mean number of books.
Solution:
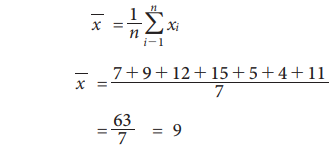
Hence the mean of the number of books is 9
Short-cut Method to find A.M.
Under this method an assumed mean or an arbitrary value (denoted by A) is used as the basis of calculation of deviations (di) from individual values. That is if di = xi – A
Then
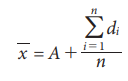
Example 5.2
A student’s marks in 5 subjects are 75, 68, 80, 92, 56. Find the average of his marks.
Solution:
Let us take the assumed mean, A = 68
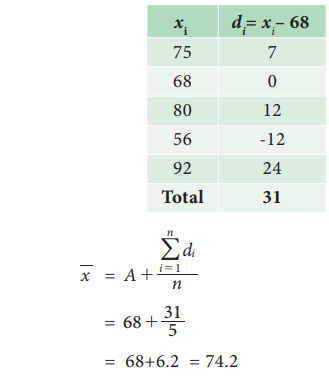
The arithmetic mean of average marks is 74.2
(b) To find A.M. for Discrete Grouped data
If x1, x2, ..., xn are discrete values with the corresponding frequencies f1, f2, …, fn. Then the mean for discrete grouped data is defined as (direct method)
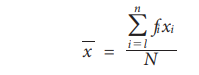
In the short cut method the formula is modified as
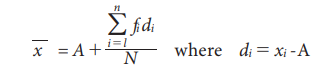
Example 5.3
A proof reads through 73 pages manuscript The number of mistakes found on each of the pages are summarized in the table below Determine the mean number of mistakes found per page

Solution:
(i) Direct Method
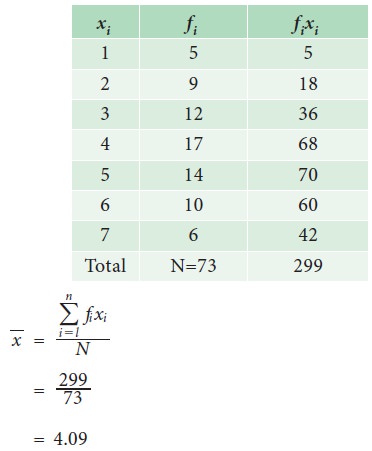
The mean number of mistakes is 4.09
(ii) Short-cut Method

The mean number of mistakes = 4.09
(c) Mean for Continuous Grouped data:
For the computation of A.M for the continuous grouped data, we can use direct method or short cut method.
Direct Method:
The formula is

Short cut method

Example 5.4
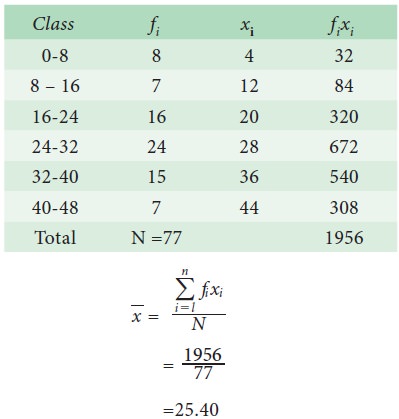
The following the distribution of persons according to different income groups

Find the average income of the persons.
Solution :
Direct Method:
Short cut method:
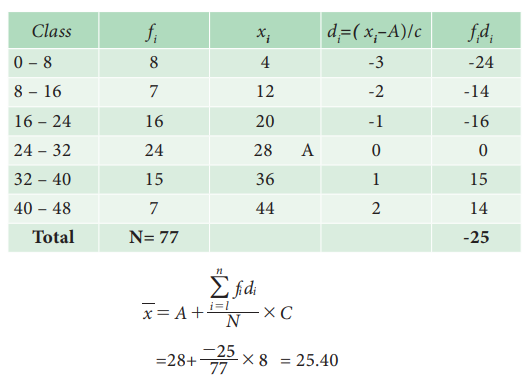
Merits
· It is easy to compute and has a unique value.
· It is based on all the observations.
· It is well defined.
· It is least affected by sampling fluctuations.
· It can be used for further statistical analysis.
Limitations
· The mean is unduly affected by the extreme items (outliers).
· It cannot be determined for the qualitative data such as beauty, honesty etc.
· It cannot be located by observations on the graphic method.
When to use?
Arithmetic mean is a best representative of the data if the data set is homogeneous. On the other hand if the data set is heterogeneous the result may be misleading and may not represent the data.
Weighted Arithmetic Mean
The arithmetic mean, as discussed earlier, gives equal importance (or weights) to each observation in the data set. However, there are situations in which values of individual observations in the data set are not of equal importance. Under these circumstances, we may attach, a weight, as an indicator of their importance to each observation value.
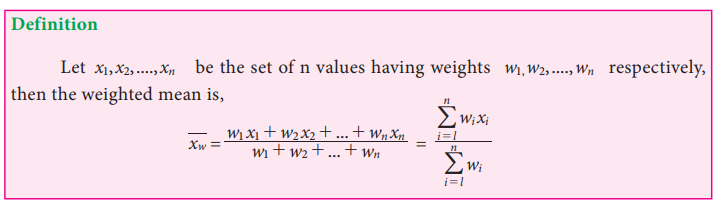
Uses of weighted arithmetic mean
Weighted arithmetic mean is used in:
· The construction of index numbers.
· Comparison of results of two or more groups where number of items in the groups differs.
· Computation of standardized death and birth rates.
Example 5.5
The weights assigned to different components in an examination or Component Weightage Marks scored
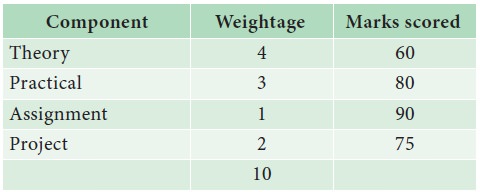
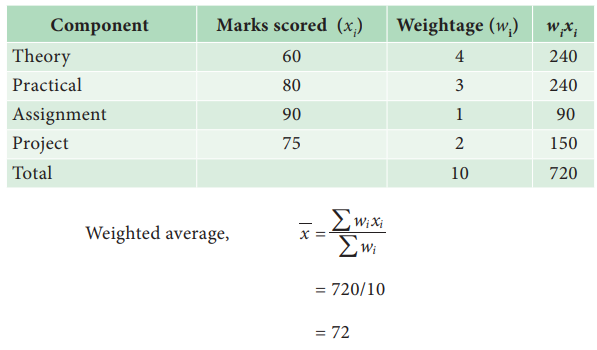
Calculate the weighted average score of the student who scored marks as given in the table
Solution:
Combined Mean:
Let ![]() 1 and
1 and ![]() 2 are the arithmetic mean of two groups (having the same unit of measurement of a variable), based on n1 and n2 observations respectively. Then the combined mean can be calculated using
2 are the arithmetic mean of two groups (having the same unit of measurement of a variable), based on n1 and n2 observations respectively. Then the combined mean can be calculated using
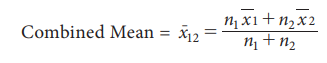
Remark : The above result can be extended to any number of groups.
Example 5.6
A class consists of 4 boys and 3 girls. The average marks obtained by the boys and girls are 20 and 30 respectively. Find the class average.
Solution:
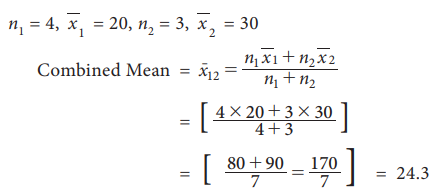
Various measures of central tendency
Related Topics