Mass property calculations

Mass property calculations

The first step in finding mass properties is to set up the location of the X, Y, and Z axis. The correctness of the calculations will depend completely on the knowledge used in choosing the axis. Hypothetically, these axes can be at any position relative to the object being considered, offered the axes are equally perpendicular. But, in reality, except the axes are chosen to be at a position that can be precisely measured and identified, the calculations are meaningless.

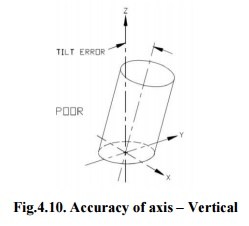
Fig.4.10. Accuracy of axis –Vertical

As shown in the figure 4.10, the axes do not create a best reference hence a small error in squareness of the base of the cylinder origins the object to tilt away from the vertical axis.

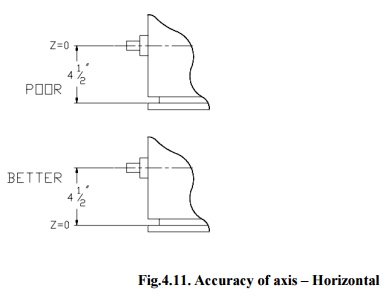
Fig.4.11. Accuracy of axis –Horizontal

An axis should always pass via a surface that is firmly linked with the bulk of the component. As shown in the figure 4.11, it would be best to position the origin (Z=0) at the end of the component rather than the fitting that is freely dimensioned virtual to the end.

1. Calculating Center of gravity location

The center of gravity of an object is:

·        described the ‘center of mass’of the object.

·        the location where the object would balance.

·        the single point where the static balance moments are all zero about three mutually perpendicular axis.

·        the centroid of object the volume when the object is homogeneous.

·        the point where the total mass of the component could be measured to be concentrated while static calculations.

·        the point about where the component rotates in free space

·        the point via the gravity force can be considered to perform

·        the point at which an exterior force must be used to create translation of an object in space

Center of gravity location is stated in units of length along the three axes (X, Y, and Z). These three components of the vector distance from the base of the coordinate system to the Center of gravity location. CG of composite masses is computed from moments considered about the origin. The essential dimensions of moment are Force and Distance. On the other hand, Mass moment may be utilized any units of Mass times Distance. For homogeneous components, volume moments may also be considered. Care should be taken to be confident that moments for all parts are defined in compatible units.

Component distances for CG position may be either positive or negative, and in reality their polarity based on the reference axis position. The CG of a homogeneous component is determined by determining the Centroid of its volume. In practical, the majority of components are not homogeneous, so that the CG must be calculated by adding the offset moments along all of the three axes.

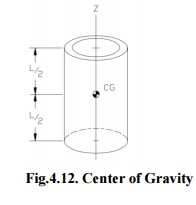
Fig.4.12. Center of Gravity