Tolerance Analysis

Tolerance Analysis

Tolerance analysis is a title to a different approaches applied in product design to know how deficiencies in parts as they are manufactured, and in assemblies, influence the ability of a product to meet customer needs. Tolerance analysis is a way of accepting how basis of deviation in part dimensions and assembly constraints distribute across parts and assemblies, and how that total deviation affects the ability of a drawing to reach its design necessities within the process capabilities of organizations and supply chains.

Tolerance openly affects the cost and performance of products. In electrical machines, safety needs that the power supply to be situated a minimum gap from adjacent components, such as one more sheet-metal component, in order to remove electrical short circuits. Tolerance analysis will describe whether the small clearances specified will meet the safety requirement, assigned manufacturing and assembly variability force on the minimum clearance.

1. Tolerance stack-up

Tolerance stack-up computations show the collective effect of part tolerance with respect to an assembly need. The tolerances ‘stacking wouldup’describe to adding tolerances to obtain total part tolerance, then evaluating that to the existing gap in order to see if the design will work suitably. This simple evaluation is also defined as ‘worst case analyses’.Worst case analysis is suitable for definite needs where failure would signify failure for a company. It is also needful and suitable for problems that occupy a low number of parts. Worst case analysis is always carried out in a single direction that is a 1-D analysis. If the analysis has part dimensions that are not parallel to the assembly measurement being defined, the stack-up approach must be edited since 2D variation such as angles, or any variation that is not parallel with the 1-D direction, does not influence the measurement of assembly with a 1-to-1 ratio.

The tolerance stacking issue occurs in the perception of assemblies from interchangeable parts because of the inability to create or join parts accurately according to nominal. Either the applicable part dimension changes around various nominal value from part by part or it is the act of assembly that directs to variation. For example, as two parts are combined through matching holes pair there is not only variation in the location of the holes relative to nominal centers on the parts but also the slippage difference of matching holes relative to each other when safe.

Thus there is the opportunity that the assembly of such interacting parts will not move or won’t come closer as planned. This can generally be judged by different assembly criteria, say G1, G2,... Here we will be discussed with just one assembly criterion, say G, which can be noted as a function of the part dimensions L1,...,Ln. A example is shown in Figure 4.7., where n = 6 and is the clearance gap of interest. It finds whether the stack of cogwheels will locate within the case or not. Thus it is preferred to have G > 0, but for performance of functional causes one may also require to limit G.

G =   L1(2 +−L3 + L4 + L5 + L6)

= L1   −− L2L3− L45 −−   L6

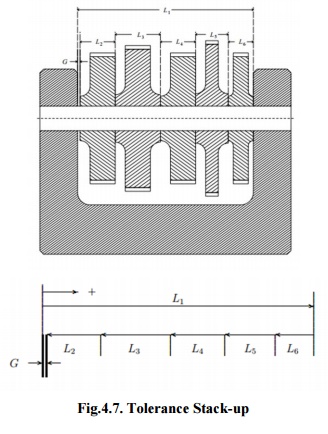
Fig.4.7. Tolerance Stack-up

As per the example, the required lengths ‘Li ‘may vary from the nominal lengths ‘λi’by a small value. If there is higher variation in the ‘Li’there may well be important problems in accepting G > 0. Thus it is sensible to limit these changes via tolerances. For similar tolerances, ‘Ti’,represent an ‘upper limit’on the absolute variation between actual and nominal values of the i th detail part dimension, it is means that |Li −λi|≤Ti. It is mostly in the interpretation of this last inequality that the different methods of tolerance stacking vary.

The nominal value ‘γ’of G is typically computed by replacing in equation L1 −L2 −L3 −L4 − L5 −L6, the actual values of Li’sby the corresponding nominal values of λi,that is γ= λ1 −λ2 −λ3 −

λ4  λ5−  λ−6.

2. Statistical method for tolerance analysis (RSS) :

In RSS method, tolerance stacking a significant new element is added to the assumptions, specifically which the detail differences from nominal are random and independent from part by part. It is expensive in the sense that it frequently commanded very close tolerances. That all variations from nominal should dispose themselves in worst case method to defer the higher assembly tolerance is a relatively unlikely proposition. On the other hand, it had the advantage of assurance the resulting assembly tolerance. Statistical tolerance in its typical form operates under two basic hypotheses:

As per Centered Normal Distribution, somewhat considering that the ‘Li’can occur anywhere within the tolerance distribution [λi−Ti, λi + Ti], assume that the ‘Li’are normal random variables, that is change randomly according to a normal distribution, centered on that similar interval and with a ±3σ distribute equal to the span of that interval, hence 99.73% of all ‘Li’values occur within this gap. As per the normal distribution is such that the ‘Li’fall with upper frequency in the middle near ‘λi’and with low frequency closer the interval endpoints. The match of the ±3σdistribution with the span of the detail tolerance span is hypothetical to state that almost all parts will satisfy the detail tolerance limits as shown in figure 4.8.

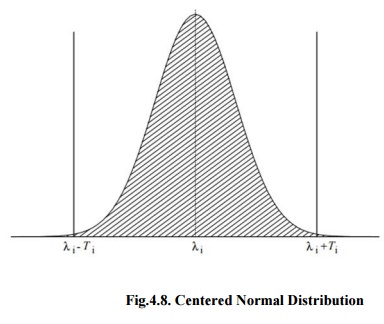
Fig.4.8. Centered Normal Distribution

Statistical tolerance stacking formula is given below:

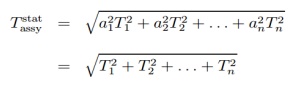
Where, a_i  = ±1 for all i = 1,...,n.

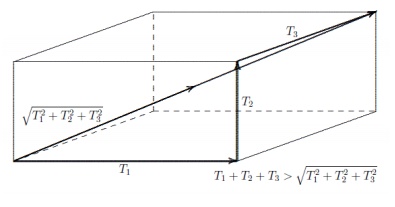
Fig.4.9. RSS cube

Typically T_{stat assy} is considerably smaller than T _{arith assy}. For n=3, the scale of this variation is simply visualized and valued by a rectangular box with side lengths T1, T2 and T3. To obtain from one corner of the box to the diagonally opposite corner, one can cross the gap T21 + T22 + T23 along that

diagonal and follow the three edges with lengths T1, T2, and T3 for a total length T arith assy = T1 + T2 + T3 as shown in figure 4.9.

3. Second Order Tolerance Analysis

Due to the manufacturing methods changing for various types of components, the distribution moments vary as well. RSS only applies standard deviation and does not contain the upper moments of skewness and kurtosis that describe the effects tool wear, form aging and other classical manufacturing situations. Second Order Tolerance Analysis includes all types of distribution moments as shown in figure 4.9

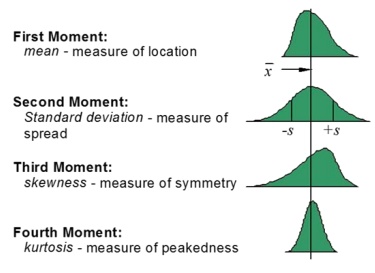
Fig.4.9. Second order Tolerance Analysis

Second Order Tolerance Analysis is required to find what output is going to be when the assembly function is not linear. In classical mechanical engineering developments kinematic changes and other assembly performances result in non-linear assembly operations. Second order estimates are more complex so manual calculations are not suitable but the computation is greatly improved and becomes feasible within tolerance analysis software.

4. Importance of Tolerance Analysis

With smaller product lifecycles, quicker to market, and higher cost pressures, the uniqueness that distinguishes a product from its competitors. Engineers are moving to the next order of resolution in order to improve cycle time and quality and to reduce costs. They are showing nearer at why they did not get the correct part and assembly dimension values they needed from manufacturing and then are trying to optimize the tolerances on the following version of the product. Optimization of tolerance during design has a high impact on the output of manufacturing, and better yields direct impact on product cost and quality. Tolerance Analysis before trying to manufacture a product helps engineers avoid time taking iterations later in the design cycle.

The electronics industry is attaining customer satisfaction purposes via a physical shrinking of their components while adding more capabilities. As electronic devices high densely packaged, the significance increases to more accurately understanding the interaction of manufacturing variation and tolerances in design. Similarly, in the aircraft, automotive and medical device productions, liability costs are increasing while environmental needs are being more forcefully forced such that companies requires to understand high precisely what may reason a failure.

Advantages of Tolerance Analysis

1.                 Accurate part assembly.

2.                 Elimination of assembly rework

3.                 Improvement in assembly quality.

4.                 Reduction of assembly cost.

5.                 High customer satisfaction.

6.  Effectiveness of out-sourcing.

Limitations of Tolerance Analysis

1.                 Time consuming process.

2.                 Skill require for complex assemblies.