Chapter: Civil : Principles of Solid Mechanics : Rings, Holes, and Inverse Problems
LameŌĆÖs Solution for Rings under Pressure
Lam├®ŌĆÖs Solution
for Rings under Pressure
A pressurized
cylindrical ring might have been discussed in previews pages since the field
equations can be integrated directly. However, since it and derivative
solutions are so elegant, practical, and intriguing because of their optimal
properties, this simple case has been reserved as an introduction to this
chapter devoted to this general class of structures.
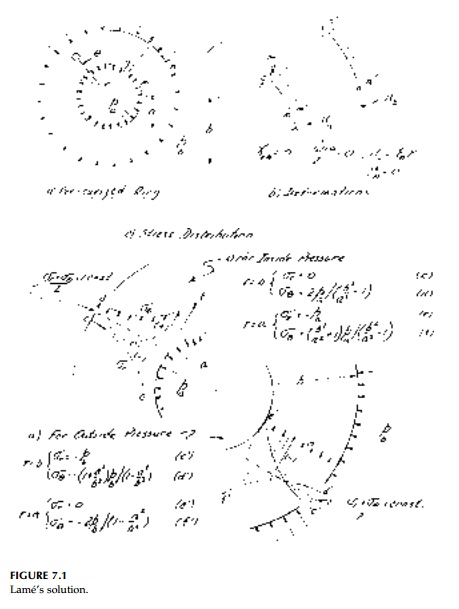
Consider a thick ring
as shown in Figure 7.1a of outer radius, b, and inner radius, a,
subjected to uniform internal and external pressures pa and pb.
This might be a transverse section in generalized plane strain cut from a
cylinder away from the ends. From symmetry, each radial line (longitudinal
section) must simply move radially along its original position the same as any
adja-cent radial line (Figure 7.1b). Therefore, nothing can be a function of ╬Ė and there is no shear strain (or stress) or elastic rotation.
Thus the equilibrium equations reduce to
a single requirement:

and from the conjugate relationship
between the first invariant and elastic rotation [Equation (5.13)]
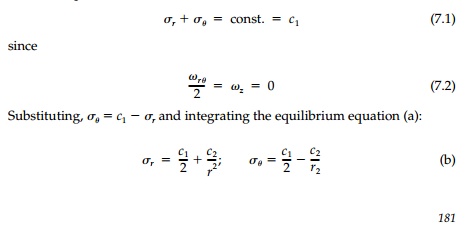

This stress
distribution for internal and external pressure considered sepa-rately is
plotted in Figure 7.1c.
The solution by the stress function
approach is equally straightforward. Since nothing can be a function of ╬Ė,
the stress function must be of type I.
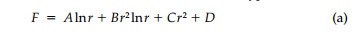
We have seen, when considering the pure bending of a ring, that the B term contributes to the displacements by introducing [Equation (6.28)] an elastic rotation Žēz= 4B╬Ė/E which is not single-valued and therefore not possible for complete rings. Therefore, taking B as zero, the stresses are:
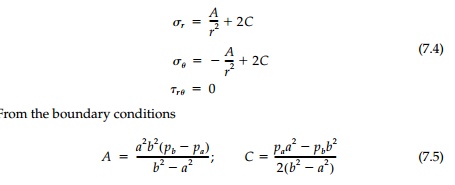
giving the same solution for the stress field [Equation (7.3)].
Since there are no shears or rotation,
all points move radially outward and
Clearly this Lam├® solution* leads to many practical applications. For thin rings b - a = t << r, the strength-of-materials approximation: Žār =0 (assumed) Žā╬Ė = (pa - pb)r/t is adequate for design. For thick-walled rings, the advantages of prestressing to apply pb to reduce the inner tensile hoop stress produced by internal pressure pa is obvious. A number of examples are given as chapter problems.
Example 7.1
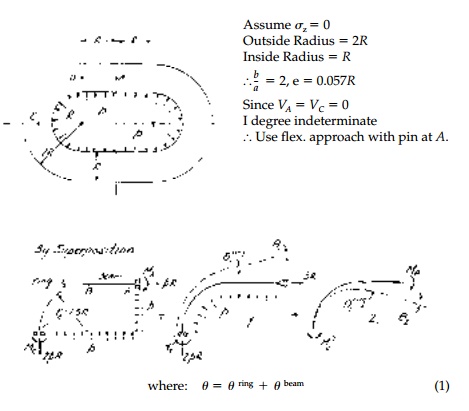
A thick, oval, cylindrical pressure
vessel has the cross-sectional dimensions shown below. Assume plane stress. By
superpoisition of elasticity solutions, determine the maximum stress and the
yield pressure.

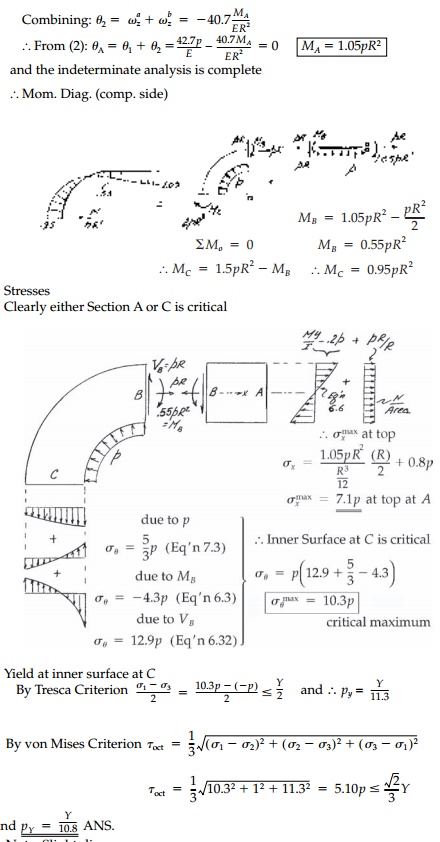
Note: Slight discrepancy at B
where the neutral axis of the beam is at the centroid and of the ring at - e
= - .057R.
However, this section is not critical and resulting error at C is, by
St. VenantŌĆÖs principle, negligible.
Related Topics