Trigonometry - Introduction | 10th Mathematics : UNIT 6 : Trigonometry
Chapter: 10th Mathematics : UNIT 6 : Trigonometry
Introduction
TRIGONOMETRY
“The deep study of nature is the most fruitful source of mathematical
discoveries”- Joseph Fourier.
French mathematician Francois Viete used trigonometry in the study of Algebra for
solving certain equations by making suitable trigonometric substitutions. His
famous formula for π can be derived with repeated use of trigonometric ratios.
One of his famous works titled Canon Mathematicus covers trigonometry; it
contains trigonometric tables, it also gives the mathematics behind the
construction of the tables, and it details how to solve both plane and
spherical triangles. He also provided the means for extracting roots and
solutions of equations of degree atmost six. Viete introduced the term
“coefficient” in mathematics. He provided a simple formula relating the roots
of a equation with its coefficients. He also provided geometric methods to
solve doubling the cube and trisecting the angle problems. He was also involved
in deciphering codes.

Learning Outcomes
·
To
recall trigonometric ratios.
·
To
recall fundamental relations between the trigonometric ratios of an angle.
·
To
recall trigonometric ratios of complementary angles.
·
To
understand trigonometric identities.
· To know methods of solving problems concerning heights and distances of various objects.
Introduction
From very ancient times surveyors, navigators and astronomers have
made use of triangles to determine distances that could not be measured
directly. This gave birth to the branch of mathematics what we call today as
“Trigonometry”.
Hipparchus of Rhodes around 200 BC(BCE), constructed a table of chord
lengths for
a circle of
circumference 360 × 60 = 21600 units which corresponds to one unit of
circumference for each minute of arc. For this achievement, Hipparchus is
considered as “The Father of Trigonometry” since it became the basis for further
development.
Indian scholars of the 5th century AD(CE), realized that working
with half-chords for half-angles greatly simplified the theory of chords and
its application to astronomy. Mathematicians like Aryabhata, the two Bhaskaras
and several others developed astonishingly sophisticated techniques for
calculating half-chord (Jya) values.
Mathematician Abu Al- Wafa of Baghdad believed to have invented
the tangent function, which he called the “Shadow”. Arabic scholars did not
know how to translate the word Jya, into their texts and simply wrote jiba as a
close approximate word.
Misinterpreting the Arabic word ‘jiba’ for ‘cove’ or ‘bay’,
translators wrote the Arabic word ‘jiba’ as ‘sinus’ in Latin to represent the
half- chord. From this, we have the name ‘sine’ used to this day. The word
“Trigonometry” itself was invented by German mathematician Bartholomaeus Pitiscus
in the beginning of 17th
century AD(CE).
Recall
Trigonometric Ratios
Let 0° < θ < 90°
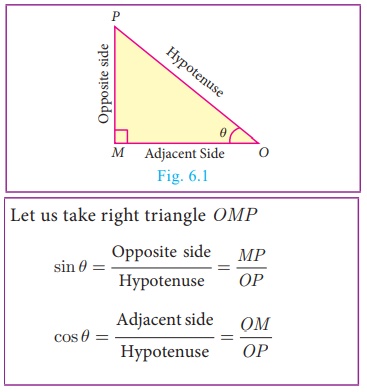
From the above two ratios we can obtain other four trigonometric
ratios as follows.
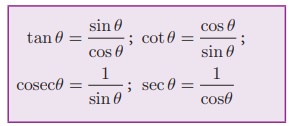
Note
All right triangles with θ as one of the
angle are similar. Hence the trigonometric ratios defined through such
right angle triangles do not depend on the triangle chosen.
Complementary angle

Visual proof of Trigonometric complementary angle
Consider a semicircle of radius 1 as shown in the figure.
Let ∠QOP = θ.
Then ∠QOR =90° − θ, so that OPQR
forms a rectangle.
From triangle OPQ , OP/OQ = cos θ
But OQ = radius = 1
Therefore OP = OQ cos θ = cos θ
Similarly, PQ/OQ = sin θ
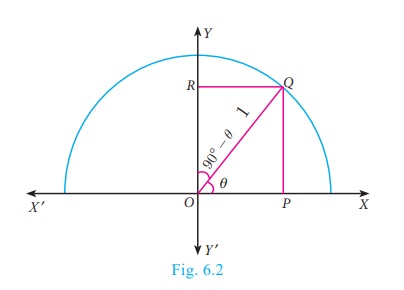
Gives, PQ = OQ sin θ = sin θ (since OQ = 1)
OP = cosθ, PQ = sinθ … (1)
Now, from triangle QOR,
we have OR/OQ = cos(90° − θ)
Therefore, OR = OQ cos(90° − θ)
So, OR = cos(90° − θ)
Similarly, RQ/OQ = sin(90° − θ)
Then, RQ = sin(90° − θ)
OR= cos(90° − θ) , RQ = sin(90° − θ) …
(2)
Since OPQR is a rectangle,
OP = RQ and OR =
PQ
Therefore from
(1) and (2) we get,

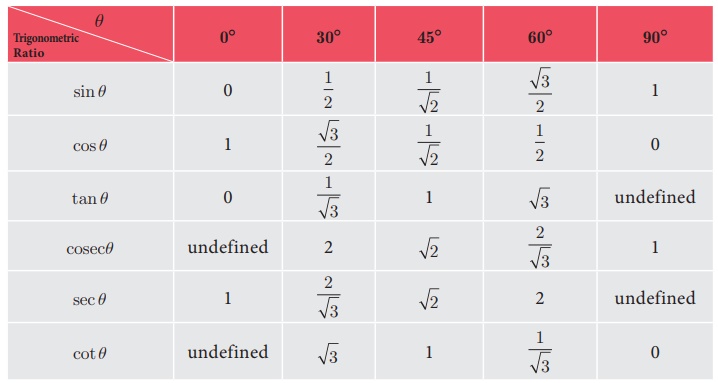
Table of Trigonometric Ratios for 0°, 30°, 45°,
60°, 90°

Related Topics