Problem Questions with Answer, Solution | Mathematics - Exercise 6.1: Trigonometric identities | 10th Mathematics : UNIT 6 : Trigonometry
Chapter: 10th Mathematics : UNIT 6 : Trigonometry
Exercise 6.1: Trigonometric identities
Exercise 6.1
1. Prove the following identities.
(i) cot θ + tan θ = sec θ cosec θ
(ii) tan 4 θ + tan2 θ = sec 4 θ − sec2 θ

2. Prove the following identities.
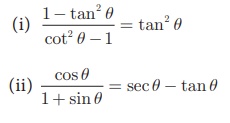

3. Prove the following identities.
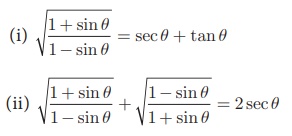

4. Prove the following identities.
(i) sec 6 θ = tan6 θ + 3 tan 2 θ sec2 θ +1
(ii) (sin θ + sec θ)2 + (cos θ + cosec θ)2 = 1 + (sec θ + cosec θ)2
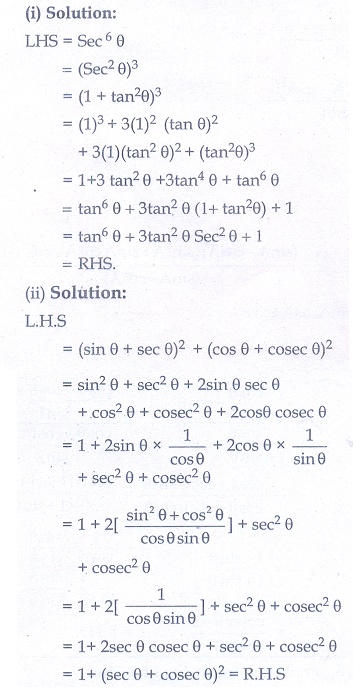
5. Prove the following identities.
(i) sec 4 θ (1 − sin 4 θ) −2 tan2 θ = 1
(ii) 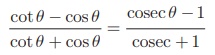

6. Prove the following identities.
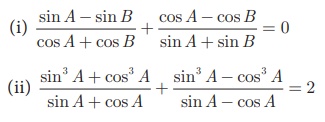

7. (i) If sin θ + cos θ = √3, then prove that tan θ + cot θ = 1.
(ii) If √3sinθ − cosθ = 0, then show that tan 3θ = (3 tan θ − tan3θ) / (1 − 3 tan2 θ)

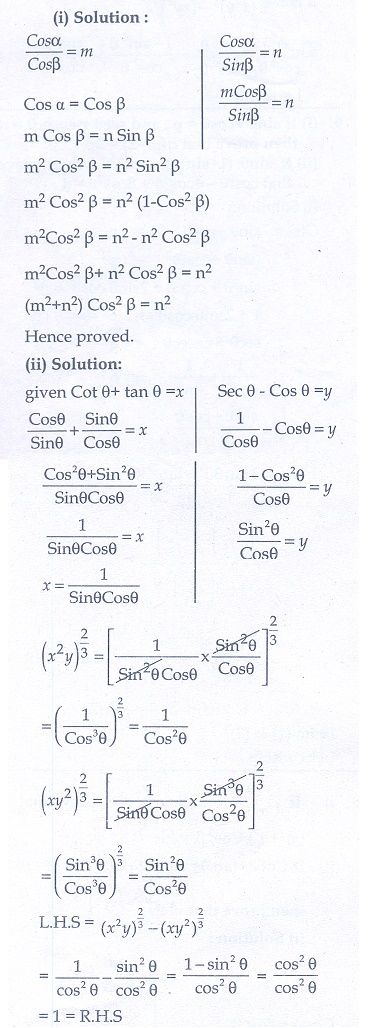
8. (i) If 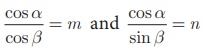 , then prove that (m2 + n2 )cos2 β = n2
, then prove that (m2 + n2 )cos2 β = n2
(ii) If cot θ + tan θ = x and sec θ − cos θ = y , then prove that (x 2y)2/3 – (xy2)2/3 = 1
9. (i) If sin θ + cos θ = p and sec θ + cosec θ = q , then prove that q ( p2 − 1) = 2p
(ii) If sin θ(1 + sin2 θ) = cos2 θ , then prove that cos6 θ − 4 cos4 θ + 8 cos2 θ = 4

10. If 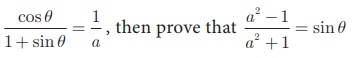
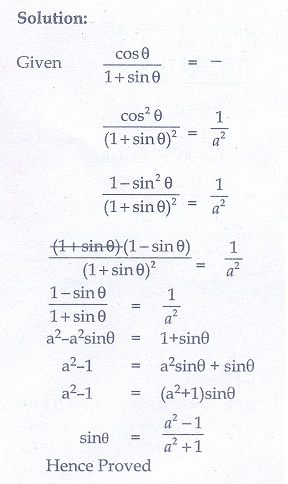
Related Topics