Problems involving Angle of Elevation and Depression

Problems involving Angle of Elevation and Depression

Let us consider the following situation.

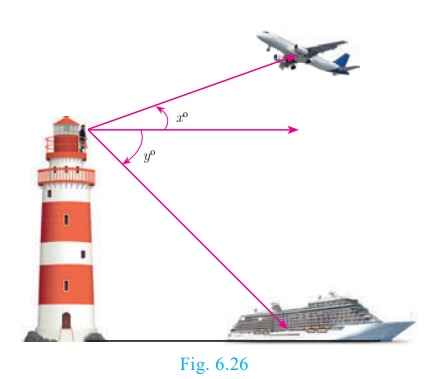
A man standing at a top of lighthouse located in a beach watch on aeroplane flying above the sea. At the same instant he watch a ship sailing in the sea. The angle with which he watch the plane correspond to angle of elevation and the angle of watching the ship corresponding to angle of depression. This is one example were one oberseves both angle of elevation and angle of depression.

In the Fig.6.26, x° is the angle of elevation and y° is the angle of depression.

In this section, we try to solve problems when Angles of elevation and depression are given.

Example 6.31

From the top of a 12 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower.

Solution

As shown in Fig.6.27, OA is the building, O is the point of observation on the top of the building OA. Then, OA = 12 m.

PP’ is the cable tower with P as the top and P ' as the bottom.

Then the angle of elevation of P, ∠MOP = 60°

And the angle of depression of P’ , ∠MOP^′ = 30°.

Suppose, height of the cable tower PP ' = h metres.

Through O, draw OM ┴ PP '

MP = PP′ − MP′ = h − OA = h −12

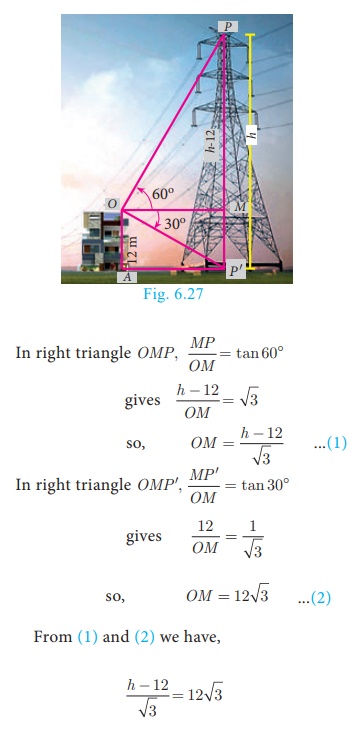
Hence, the required height of the cable tower is 48 m.

Example 6.32

A pole 5 m high is fixed on the top of a tower. The angle of elevation of the top of the pole observed from a point ‘A’ on the ground is 60° and the angle of depression to the point ‘A’ from the top of the tower is 45°. Find the height of the tower. (√3=1.732)

Solution

Let BC be the height of the tower and CD be the height of the pole.

Let ‘A’ be the point of observation.

Let BC = x and AB = y.

From the diagram,

∠BAD = 60° and ∠XCA = 45° = ∠BAC

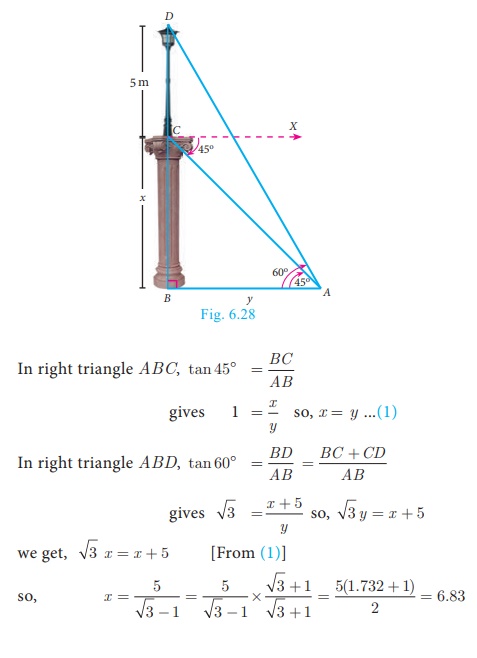
Hence, height of the tower is 6.83 m.

Example 6.33

From a window (h metres high above the ground) of a house in a street, the angles of elevation and depression of the top and the foot of another house on the opposite  side of the street are θ₁ and θ₂ respectively. Show that the height of the opposite house is .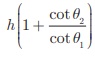

Solution

Let W be the point on the window where the angles of elevation and depression are measured. Let PQ be the house on the opposite side.

Then WA is the width of the street.

Height of the window = h metres

= AQ (WR = AQ)

Let PA = x metres.

Therefore, height of the opposite house = PA+AQ = x + h =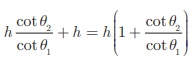 

Hence Proved.