Problems involving Angle of Depression

Problems involving Angle of Depression

In  this section, we try to solve problems when Angles of depression are given. 

Note

Angle of Depression and Angle of Elevation are equal become they are alternative angles. 

Example 6.26

A player sitting on the top of a tower of height 20 m observes the angle of epression of a ball lying on the ground as 60° . Find the distance between the foot of the tower and the ball. (√3 = 1.732)

Solution

Let BC be the height of the tower and A be the position of the ball lying on the ground. Then,

BC = 20 m and ∠XCA = 60° = ∠CAB

Let AB = x metres.

In right triangle ABC,

tan 60° = BC/AB

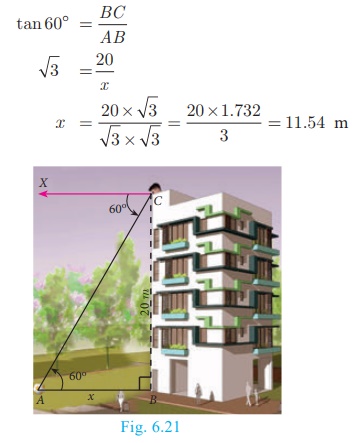
Hence, the distance between the foot of the tower and the ball is 11.54 m.

Example 6.27

The horizontal distance between two buildings is 140 m. The angle of depression of the top of the first building when seen from the top of the second building is 30° . If the height of the first building is 60 m, find the height of the second building. (√3 = 1.732)

Solution

The height of the first building AB = 60 m. Now, AB = MD = 60 m Let the height of the second building CD = h. Distance BD = 140 m 

Now, AM = BD = 140 m

From the diagram,

∠XCA = 30° = ∠CAM

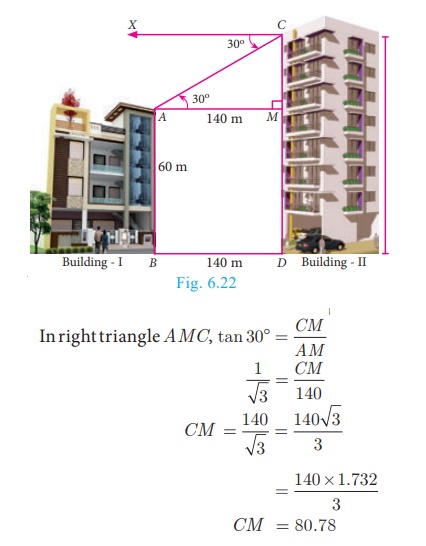
CM = 80.78

Now, h = CD = CM +MD = 80.78+60 = 140.78

Therefore the height of the second building is 140.78 m

Example 6.28

From the top of a tower 50 m high, the angles of depression of the top and bottom of a tree are observed to be 30° and 45° respectively. Find the height of the tree. (√3 = 1.732)

Solution

The height of the tower AB = 50 m

Let the height of the tree CD = y and BD = x

From the diagram, ∠XAC = 30° = ∠ACM and ∠XAD = 45° = ∠ADB

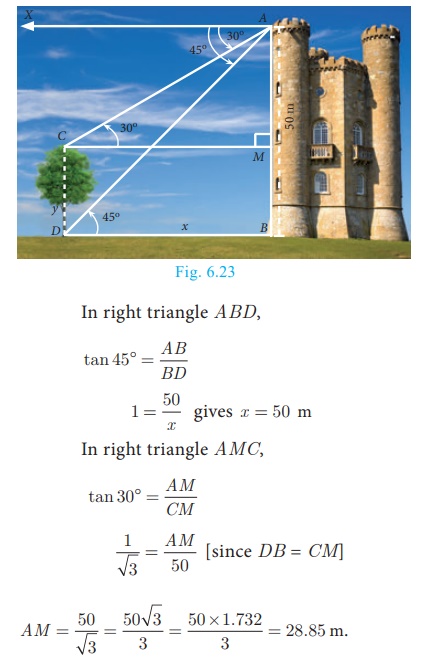
Therefore, height of the tree = CD = MB = AB −AM = 50 −28. 85 = 21. 15 m

Example 6.29

As observed from the top of a 60 m high light house from the sea level, the angles of depression of two ships are 28° and 45° . If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships. (tan 28° =0.5317)

Solution

Let the observer on the lighthouse CD be at D.

Height of the lighthouse CD = 60 m

From the diagram,

∠XDA = 28° = ∠DAC and

∠XDB = 45° = ∠DBC

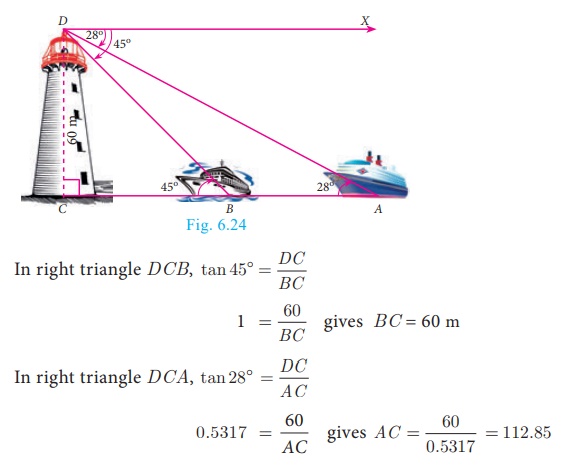
Distance between the two ships AB = AC −BC = 52.85 m

Example 6.30

A man is watching a boat speeding away from the top of a tower. The boat makes an angle of depression of 60° with the man’s eye when at a distance of 200 m from the tower. After 10 seconds, the angle of depression becomes 45°. What is the approximate speed of the boat (in km / hr), assuming that it is sailing in still water? (√3 = 1.732)

Solution

Let AB be the tower.

Let C and D be the positions of the boat.

From the diagram,

∠XAC = 60° = ∠ACB and

∠XAD = 45° = ∠ADB , BC = 200 m

In right triangle ABC, tan 60° = AB/BC

gives √3 = AB /200

 we get AB = 200√3 ...(1)

In right triangle ABD, tan 45° = AB/BD

Gives 1 = 200√3 / BD     [by (1) ]

we get, BD = 200√3

Now, CD =  BD − BC

 CD = 200√3 − 200 = − 200(√3 – 1) = 146 4.

It is given that the distance CD is covered in 10 seconds.

That is, the distance of 146.4 m is covered in 10 seconds.

Therefore, speed of the boat = distance / time

= 146.4 / 10  = 14. 64 m/s gives 14. 64 × (3600/1000) km/hr = 52. 704 km/hr