Problem Questions with Answer, Solution | Trigonometry - Exercise: Trigonometry | 10th Mathematics : UNIT 6 : Trigonometry
Chapter: 10th Mathematics : UNIT 6 : Trigonometry
Exercise: Trigonometry
Unit Exercise
1. Prove that
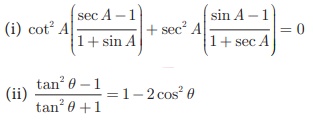
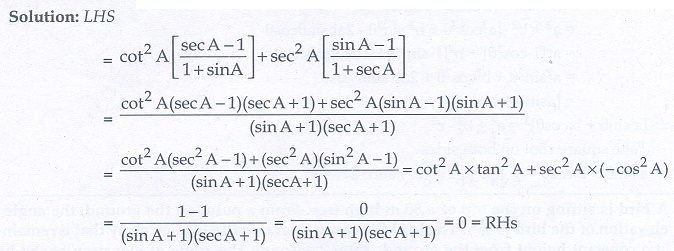
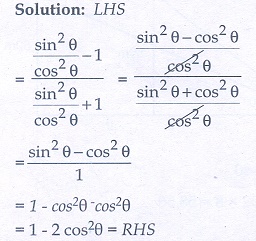
2. Prove that 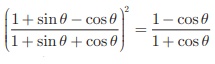
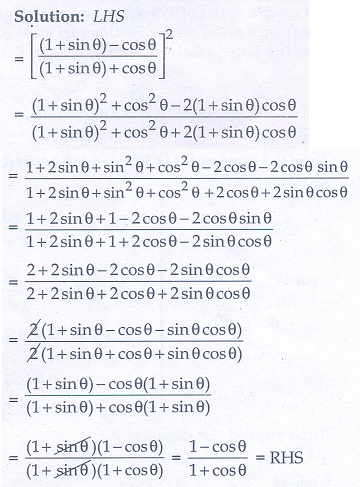
3. If x sin 3θ + y cos3 θ = sin θ cos θ and x sin θ = y cos θ , then prove that x2 + y2 = 1.
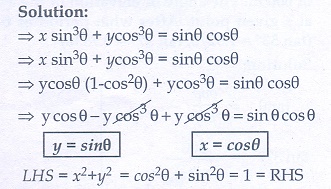
4. If a cos θ − b sin θ = c , then prove that (a sin θ + b cos θ) = ± √[a 2 +b2 −c2 ]

5. A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45° . The bird flies away horizontally in such away that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30° . Determine the speed at which the bird flies. (√3 = 1.732)

6. An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37° at a given point. After what period of time does the angle of elevation increase to 53° ? (tan 53° = 1.3270, tan 37° = 0. 7536)

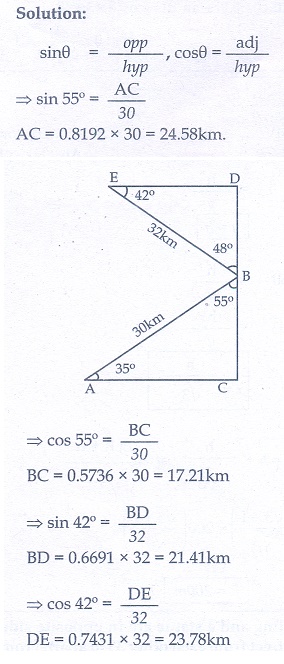
7. A bird is flying from A towards B at an angle of 35° , a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away.
(i) How far is B to the North of A?
(ii) How far is B to the West of A?
(iii) How far is C to the North of B?
(iv) How far is C to the East of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
8. Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is 200 ( (√3+ 1) / √3) metres, find the height of the lighthouse.

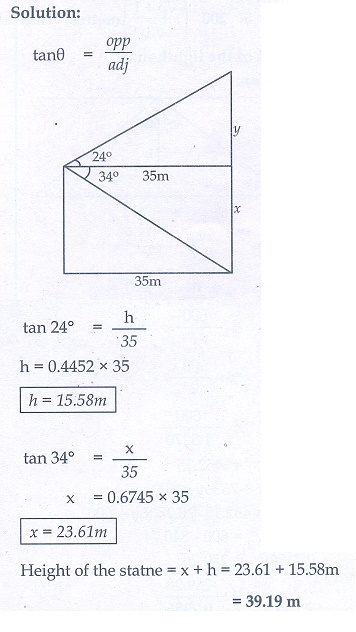
9. A building and a statue are in opposite side of a street from each other 35 m apart. From a point on the roof of building the angle of elevation of the top of statue is 24° and the angle of depression of base of the statue is 34° . Find the height of the statue. (tan 24° = 0.4452, tan 34° = 0.6745)
5. 29.28 m/s
6. 1.97 seconds (approx)
7.(i) 24.58 km(approx) (ii) 17.21 km (approx) (iii) 21.41 km (approx) (iv) 23.78 km (approx)
8. 200 m
9. 39.19 m
Related Topics