Implementation of trees

Describe in detail about the implementation of trees

One way to implement a tree would be to have in each node, besides its data, a link to each child of the node. However, since the number of children per node can vary so greatly and is not known in advance, it might be infeasible to make the children direct links in the data

Node declarations for trees:

1 struct TreeNode

2 {

3 Object element;

4 TreeNode *firstChild;

5 TreeNode *nextSibling;

};

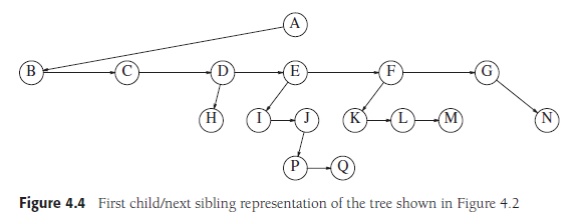
structure, because there would be too much wasted space. The solution is simple: Keep the children of each node in a linked list of tree nodes. The declaration is typical. Figure 4.4 shows how a tree might be represented in this implementation. Horizontal arrows that point downward are firstChild links. Arrows that go left to right are nextSibling links. Null links are not drawn, because there are too many. In the tree of Figure 4.4, node E has both a link to a sibling (F) and a link to a child (I), while some nodes have neither.

Tree Traversals with an Application

There are many applications for trees. One of the popular uses is the directory structure in many common operating systems, including UNIX and DOS. Figure 4.5 is a typical directory in the UNIX file system. The root of this directory is /usr. (The asterisk next to the name indicates that /usr is itself a directory.) /usr has three children, mark, alex, and bill, which are themselves directories. Thus, /usr contains three directories and no regular files. The filename /usr/mark/book/ch1.r is obtained by following the leftmost child three times. Each / after the first indicates an edge; the result is the full pathname. This hierarchical file system is very popular because it allows users to organize their data logically. Furthermore, two files in different directories can share the same name, because they must have different paths from the root and thus have different pathnames. A directory in the UNIX file system is just a file with a list of all its children, so the directories are structured almost exactly in accordance

with the type declaration above.1 Indeed, on some versions of UNIX, if the normal command to print a file is applied to a directory, then the names of the files in the directory can be seen in the output (along with other non-ASCII information). Suppose we would like to list the names of all of the files in the directory. Our output format will be that files that are depth di will have their names indented by di tabs. Our algorithm is given in Figure 4.6 as pseudocode. The recursive function listAll needs to be started with a depth of 0 to signify no indenting for the root. This depth is an internal bookkeeping variable, and is hardly a parameter that a calling routine should be expected to know about. Thus, the default value of 0 is provided for depth. The logic of the algorithm is simple to follow. The name of the file object is printed out with the appropriate number of tabs. If the entry is a directory, then we process all children recursively, one by one. These children are one level deeper, and thus need to be indented an extra space. This traversal strategy is known as a preorder traversal. In a preorder traversal, work at a node is performed before (pre) its children are processed. When this program is run, it is clear that line 1 is executed exactly once per node, since each name is output once. Since line 1 is executed at most once per node, line 2 must also be executed once per node. Furthermore, line 4 can be executed at most once for each child of each node. But the number of children is exactly one less than the number of nodes. Finally, the for loop iterates once per execution of line 4 plus once each time the loop ends. Thus, the total amount of work is constant per node. If there are N file names to be output, then the running time is O(N). Another common method of traversing a tree is the postorder traversal. In a postorder traversal, the work at a node is performed after (post) its children are evaluated. As an example, Figure 4.8 represents the same directory structure as before, with the numbers in parentheses representing the number of disk blocks taken up by each file. Since the directories are themselves files, they have sizes too. Suppose we would like to calculate the total number of blocks used by all the files in the tree. The most natural way to do this would be to find the number of blocks contained in the subdirectories /usr/mark (30), /usr/alex (9), and /usr/bill (32). The total number of blocks is then the total in

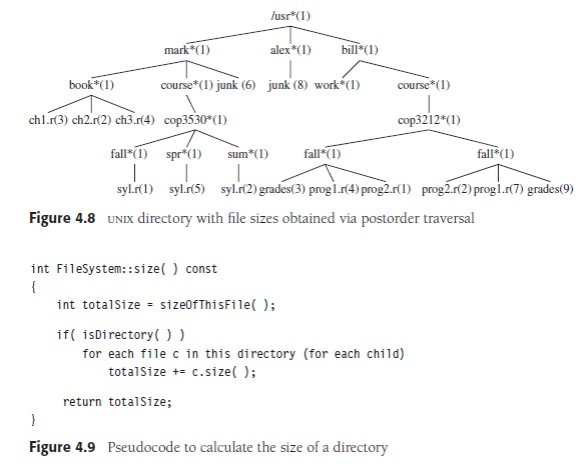
subdirectories plus the one block used by /usr, for a total of 72. The pseudocode method size in Figure 4.9 implements this strategy. If the current object is not a directory, then size merely returns the number of blocks it uses in the current object. Otherwise, the number of blocks used by the directory is added to the number of blocks (recursively) found in all the children.