Application of Depth First Search

Give the application of Depth First Search

Depth-first search is a generalization of preorder traversal. Starting at some vertex, v, we process v and then recursively traverse all vertices adjacent to v. If this process is performed on a tree, then all tree vertices are systematically visited in a total of O(|E|) time, since |E| = _(|V|). If we perform this process on an arbitrary graph, we need to be careful to avoid cycles. To do this, when we visit a vertex, v, we mark it visited, since now we have been there, and recursively call depth-first search on all adjacent vertices that are not already marked. We implicitly assume that for undirected graphs every edge (v, w) appears twice in the adjacency lists: once as (v, w) and once as (w, v). The procedure in Figure 9.61 performs a depth-first search (and does absolutely nothing else) and is a template for the general style. For each vertex, the data member visited is initialized to false. By recursively calling the procedures only on nodes that have not been visited, we guarantee that we do not loop indefinitely. If the graph is undirected and not connected, or directed and not strongly connected, this strategy might fail to visit some nodes. We then search for an unmarked node,

void Graph::dfs( Vertex v )

{

v.visited = true;

for each Vertex w adjacent to v

if( !w.visited )

dfs( w );

}

Template for depth-first search (pseudocode)

apply a depth-first traversal there, and continue this process until there are no unmarked nodes.2 Because this strategy guarantees that each edge is encountered only once, the total time to perform the traversal is O(|E| + |V|), as long as adjacency lists are used.

Implementation: Undirected Graphs

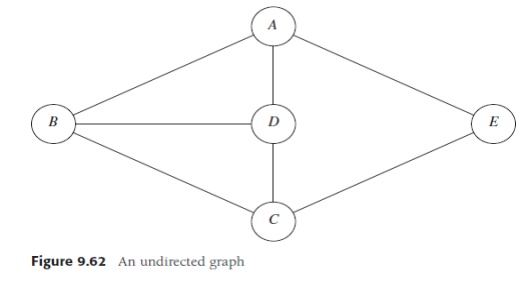
An undirected graph is connected if and only if a depth-first search starting from any node visits every node. Because this test is so easy to apply, we will assume that the graphs we deal with are connected. If they are not, then we can find all the connected components and apply our algorithm on each of these in turn. As an example of depth-first search, suppose in the graph of Figure 9.62 we start at vertex A. Then we mark A as visited and call dfs(B) recursively. dfs(B) marks B as visited and calls dfs(C) recursively. dfs(C) marks C as visited and calls dfs(D) recursively. dfs(D) sees both A and B, but both of these are marked, so no recursive calls are made. dfs(D) also sees that C is adjacent but marked, so no recursive call is made there, and dfs(D) returns back to dfs(C). dfs(C) sees B adjacent, ignores it, finds a previously unseen vertex E adjacent, and thus calls dfs(E). dfs(E) marks E, ignores A and C, and returns to dfs(C). dfs(C) returns to dfs(B). dfs(B) ignores both A and D and returns. dfs(A) ignores both D and E and returns. (We have actually touched every edge twice, once as (v, w) and again as (w, v), but this is really once per adjacency list entry.)

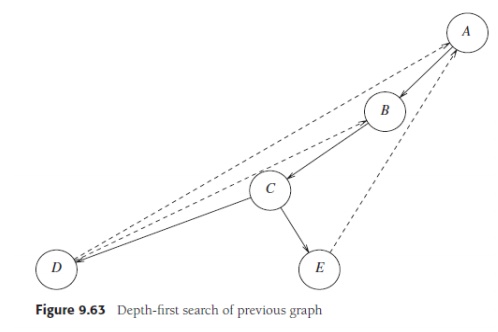
We graphically illustrate these steps with a depth-first spanning tree. The root of the tree is A, the first vertex visited. Each edge (v, w) in the graph is present in the tree. If, when we process (v, w), we find that w is unmarked, or if, when we process (w, v), we find that v is unmarked, we indicate this with a tree edge. If, when we process (v, w), we find that w is already marked, and when processing (w, v), we find that v is already marked, we draw a dashed line, which we will call a back edge, to indicate that this “edge” is not really part of the tree. The depth-first search of the graph in Figure 9.62 is shown in Figure 9.63. The tree will simulate the traversal we performed. A preorder numbering of the tree, using only tree edges, tells us the order in which the vertices were marked. If the graph is not connected, then processing all nodes (and edges) requires several calls to dfs, and each generates a tree. This entire collection is a depth-first spanning forest.