Implementation of a Binary Tree with an expression tree

What is a Binary Tree? Explain the implementation of a Binary Tree with an expression tree

A binary tree is a tree in which no node can have more than two children. Figure 4.11 shows that a binary tree consists of a root and two subtrees, TL and TR, both of which could possibly be empty. A property of a binary tree that is sometimes important is that the depth of an average binary tree is considerably smaller than N. 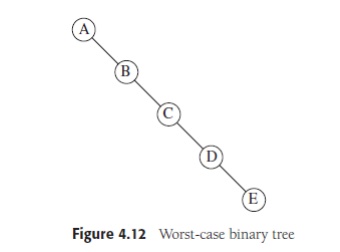An analysis shows that the average depth is O(√N), and that for a special type of binary tree, namely the binary search tree, the average value of the depth is O(logN). Unfortunately, the depth can be as large as N − 1, as the example in Figure 4.12 shows.

ch1.r 3

ch2.r 2

ch3.r 4

book 10

syl.r 1

fall 2

syl.r 5

spr 6

syl.r 2

sum 3

cop3530 12

course 13

junk 6

mark 30

junk 8

alex 9

work 1

grades 3

prog1.r 4

prog2.r 1

fall 9

prog2.r 2

prog1.r 7

grades 9

fall 19

cop3212 29

course 30 bill 32

/usr 72

Implementation

Because a binary tree node has at most two children, we can keep direct links to them. The declaration of tree nodes is similar in structure to that for doubly linked lists, in that a node is a structure consisting of the element information plus two pointers (left and right) to other nodes(Figure 4.13). We could draw the binary trees using the rectangular boxes that are customary for linked lists, but trees are generally drawn as circles connected by lines, because they are actually graphs. We also do not explicitly draw nullptr links when referring to trees, because every binary tree with N nodes would require N + 1 nullptr links. Binary trees have many important uses not associated with searching. One of the principal uses of binary trees is in the area of compiler design, which we will now explore.

Example: Expression Trees

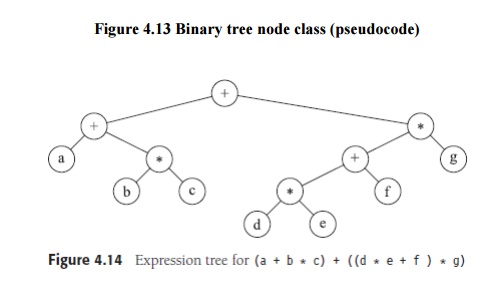
Figure 4.14 shows an example of an expression tree. The leaves of an expression tree are operands, such as constants or variable names, and the other nodes contain operators. This particular tree happens to be binary, because all the operators are binary, and although this is the simplest case, it is possible for nodes to have more than two children. It is also possible for a node to have only one child, as is the case with the unary minus operator. We can evaluate an expression tree, T, by applying the operator at the root to the values struct BinaryNode

{

Object element; // The data in the node

BinaryNode *left; // Left child

BinaryNode *right; // Right child

};

obtained by recursively evaluating the left and right subtrees. In our example, the left subtree evaluates to a + (b * c) and the right subtree evaluates to ((d * e) + f) * g. The entire tree therefore represents (a + (b * c)) + (((d * e) + f) * g). We can produce an (overly parenthesized) infix expression by recursively producing a parenthesized left expression, then printing out the operator at the root, and finally recursively producing a parenthesized right expression. This general strategy (left, node, right) is known as an inorder traversal; it is easy to remember because of the type of expression it produces. An alternate traversal strategy is to recursively print out the left subtree, the right subtree, and then the operator. If we apply this strategy to our tree above, the output is a b c * + d e * f + g * +, which is easily seen to be the postfix representation. This traversal strategy is generally known as a postorder traversal. A third traversal strategy is to print out the operator first and then recursively print out the left and right subtrees. The resulting expression, + + a * b c * + * d e f g, is the less useful prefix notation, and the traversal strategy is a preorder traversal