Binary tree and Types of binary trees

Binary tree

A simple binary tree of size 9 and height 3, with a root node whose value is 2. The above tree is unbalanced and not sorted. In computer science, a binary tree is a treedata structure in which each node has at most two children (referred to as the left child and the right child). In a binary tree, the degree of each node can be at most two. Binary trees are used to implement binary search trees and binary heaps, and are used for efficient searching and sorting. A binary tree is a special case of a Kary tree, where k is 2.

Types of binary trees

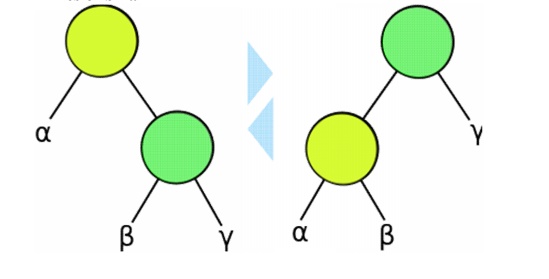
Tree rotations are very common internal operations on self-balancing binary trees.

A rooted binary tree is a tree with a root node in which every node has at most two children.

•  A full binary tree (sometimes 2-tree or strictly binary tree) is a tree in which every node other than the leaves has two children. A full tree is sometimes ambiguously defined as a perfect tree. Physicists define a binary tree to mean a full binary tree.[1]

• A  proper binary tree is an ordered tree in which each internal node has exactly two children.

•  A perfect binary tree is a full binary tree in which all leaves have the same depth or same level, and in which every parent has two children.[2] (This is ambiguously also called a complete binary tree (see next).) An example of a perfect binary tree is the ancestry chart of a person to a given depth, as each person has exactly two biological parents (one mother and one father); note that this reverses the usual parent/child tree convention, and these trees go in the opposite direction from usual (root at bottom).

•   A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.[3] A tree is called an almost complete binary tree or nearly complete binary tree if the exception holds, i.e. the last level is not completely filled. This type of tree is used as a specialized data structure called a heap.

•  An infinite complete binary tree is a tree with a countably infinite number of levels, in which every node has two children, so that there are 2d nodes at level d. The set of all nodes is countably infinite, but the set of all infinite paths from the root is uncountable, having the cardinality of the continuum. These paths correspond by an order-preserving bijection to the points of the Cantor set, or (using the example of a Stern–Brocot tree) to the set of positive irrational numbers.

•  A balanced binary tree is commonly defined as a binary tree in which the depth of the left and right subtrees of every node differ by 1 or less,[4] although in general it is a binary tree where no leaf is much farther away from the root than any other leaf. (Different balancing schemes allow different definitions of "much farther".[5]) Binary trees that are balanced according to this definition have a predictable depth (how many nodes are traversed from the root to a leaf, counting the root as node 0 and subsequent nodes as 1, 2, ...,n). This depth (also called the height) is equal to the integer part of log2(n), where n is the number of nodes on the balanced tree. For example, for a balanced tree with only 1 node, log2(1) = 0, so the depth of the tree is 0. For a balanced tree with 100 nodes, log2(100) = 6.64, so it has a depth of 6.

•  A degenerate (or pathological) tree is a tree where each parent node has only one associated child node. This means that performance-wise, the tree will behave like a linked list data structure.

Note that this terminology often varies in the literature, especially with respect to the meaning of "complete" and "full".