Common operations of binary trees

Common operations

There are a variety of different operations that can be performed on binary trees. Some are mutator operations, while others simply return useful information about the tree.

Insertion

Nodes can be inserted into binary trees in between two other nodes or added after a leaf node. In binary trees, a node that is inserted is specified as to which child it is.

External nodes

Say that the external node being added onto is node A. To add a new node after node A, A assigns the new node as one of its children and the new node assigns node A as its parent.

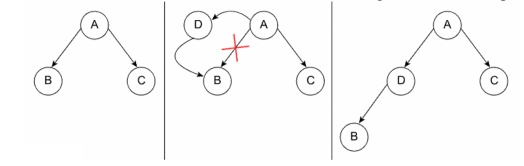
Internal nodes

The process of inserting a node into a binary tree Insertion on internal nodes is slightly more complex than on external nodes. Say that the internal node is node A and that node B is the child of A. (If the insertion is to insert a right child, then B is the right child of A, and similarly with a left child insertion.) A assigns its child to the new node and the new node assigns its parent to A. Then the new node assigns its child to B and B assigns its parent as the new node.

Deletion

Deletion is the process whereby a node is removed from the tree. Only certain nodes in a binary tree can be removed unambiguously,

Node with zero or one children

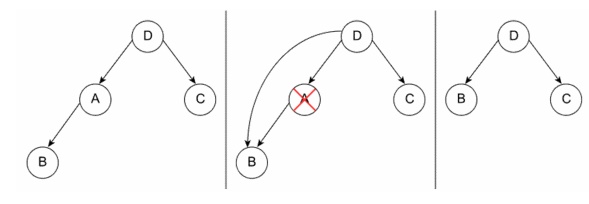
The process of deleting an internal node in a binary tree Say that the node to delete is node A. If a node has no children (external node), deletion is accomplished by setting the child of A's parent to null. If it has one child, set the parent of A's child to A's parent and set the child of A's parent to A's child.

Node with two children

In a binary tree, a node with two children cannot be deleted unambiguously.[7] However, in certain binary trees (including binary search trees) these nodes can be deleted, though with a rearrangement of the tree structure.

Traversal

Pre-order, in-order, and post-order traversal visit each node in a tree by recursively visiting each node in the left and right subtrees of the root.

Depth-first order

In depth-first order, we always attempt to visit the node farthest from the root node that we can, but with the caveat that it must be a child of a node we have already visited. Unlike a depth-first search on graphs, there is no need to remember all the nodes we have visited, because a tree cannot contain cycles. Pre-order is a special case of this. See depth-first search for more information.

Breadth-first order

Contrasting with depth-first order is breadth-first order, which always attempts to visit the node closest to the root that it has not already visited. See breadth-first search for more information. Also called a level-order traversal. In a complete binary tree, a node's breadth-index (i - (2d - 1)) can be used as traversal instructions from the root. Reading bitwise from left to right, starting at bit d - 1, where d is the node's distance from the root (d = floor(log2(i+1))) and the node in question is not the root itself (d > 0). When the breadth-index is masked at bit d - 1, the bit values 0 and 1 mean to step either left or right, respectively. The process continues by successively checking the next bit to the right until there are no more. The rightmost bit indicates the final traversal from the desired node's parent to the node itself. There is a time-space trade-off between iterating a complete binary tree this way versus each node having pointer/s to its sibling/s.

Encoding general trees as binary trees

There is a one-to-one mapping between general ordered trees and binary trees, which in particular is used by Lisp to represent general ordered trees as binary trees. To convert a general ordered tree to binary tree, we only need to represent the general tree in left child right sibling way. The result of this representation will be automatically binary tree, if viewed from a different perspective. Each node N in the ordered tree corresponds to a node N' in the binary tree; the left child of N' is the node corresponding to the first child of N, and the right child of N' is the node corresponding to N 's next sibling --- that is, the next node in order among the children of the parent of N. This binary tree representation of a general order tree is sometimes also referred to as a left child-right sibling binary tree (LCRS tree), or a doubly chained tree, or a Filial-Heir chain. One way of thinking about this is that each node's children are in a linked list, chained together with their right fields, and the node only has a pointer to the beginning or head of his list, through its left field. For example, in the tree on the left, A has the 6 children {B,C,D,E,F,G}. It can be converted into the binary tree on the right.

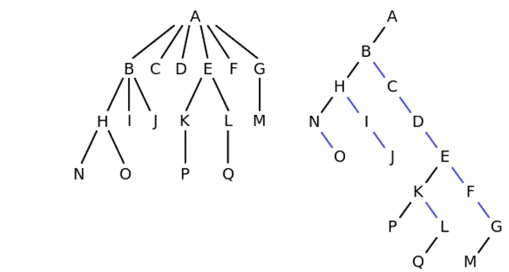
The binary tree can be thought of as the original tree tilted sideways, with the black left edges representing first child and the blue right edges representing next sibling. The leaves of the tree on the left would be written in Lisp as:

(((N O) I J) C D ((P) (Q)) F (M))

which would be implemented in memory as the binary tree on the right, without any letters on those nodes that have a left child.

Binary Trees

A binary tree is composed of zero or more nodes

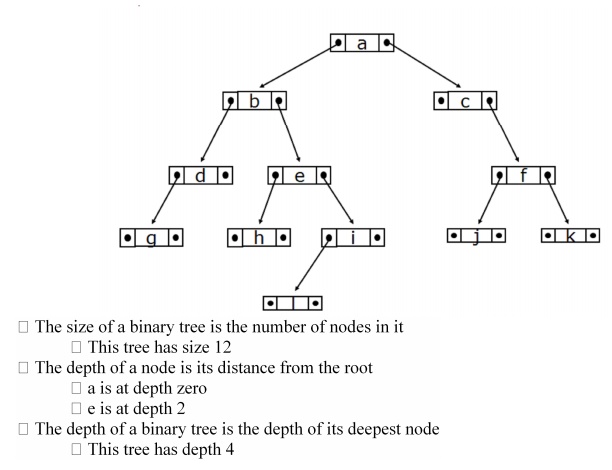
Preorder traversal