Graph Representations and Traversals - Tree

Graph Representations and Traversals

A directed graph G is an ordered pair (V, E ) consisting of a set of vertices or nodes V = {v1,...,vn} and a set of edges or arcs E ⊆ V 2. Generally we denote the number of vertices by |V | or nand the number of edges by |E | or m. Directed graphs are commonly represented as an adjacency list, which comprises an array or list of vertices, where each vertex vi stores a list of all the vertices vj for which there is an edge (vi, vj) ∈ E.

Another common representation is an adjacency matrix, which is a two-dimensional array, where Ai j is non-zero when there is an edge (vi, vj) ∈ E. In practice, many graphs are sparse in the sense that most of the possible edges between pairs of vertices do not exist, i.e. m << n2. In such cases the adjacency list is generally preferable to the adjacency matrix representation. Edges can sometimes additionally have an integer  weight, which can be used to represent distances or costs.

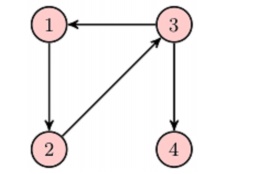
Here is a simple directed graph with four vertices V = {1, 2, 3, 4} and four edges E = {(1, 2), (2, 3), (3, 1), (3, 4)}. Consider the following abstract data type for a directed graph with weighted edges. Note that while this specification does not explicitly require any particular implementation, the required running times of some of these functions constrain the implementation in various ways. For instance, a naive adjacency matrix implementation would take Θ(n2) time to consider every array entry in producing a list of all the edges. However the edges function is required to do this in O(n + m) time.

(* A signature for directed graphs.*)

type graph (* A directed graph consisting of a set of vertices * V and directed edges E with integer weights. *)

type vertex (* A vertex, or node, of the graph *) type edge (* A edge of the graph *)

(* Creates an empty graph. *) val create : unit -> graph

(* Returns the id of the specified vertex. *) valvertex_id : vertex ->int

(* Compares two vertices, returning 0 if their ids are equal, -1 if

*  the first has a smaller id, and +1 if first has a larger id.

*  Suitable for comparators in sets and maps. *)

val compare : vertex -> vertex ->int

(* For an edge return (src, dst, w) where src is the source vertex of

*  the edge, dst is the destination vertex, and w is the edge

*  weight. *)

valedge_info : edge -> vertex * vertex * int

(* True if the given graph is empty (has no vertices). * Run time O(1). *)

valis_empty : graph -> bool

(* A list of all vertices in the graph, without duplicates, in the order

*  they were added.Run time: O(|V|). *) val vertices : graph -> vertex list

(* A list of all vertices in the graph, without duplicates, in the order

*  they were added.Run time: O(1). *)

valnum_vertices : graph ->int

(* A list of all edges in the graph, without duplicates.

*  Run time: O(|V|+|E|). *) val edges : graph -> edge list

(* A list of the edges leaving the vertex v.

*  Run time: linear in the length of the result. *)

val outgoing : vertex -> edge list

(* A list of the edges coming in to the vertex v.

*  Run time: linear in the length of the result. *) val incoming : vertex -> edge list

(* The number of incoming edges for the specified vertex.

*  Run time: O(1). *)

valin_degree : vertex ->int

(* The number of outgoing edges for the specified vertex. * Run time: O(1). *)

valout_degree : vertex ->int

(* Adds a new isolated vertex (a vertex with no incident

*  edges) to the specified graph, and returns that vertex.

Run time: O(1). *)

valadd_vertex : graph -> vertex

(* Removes the specified vertex from the specified graph,

*  along with all incident edges; that is, all edges that

*  have the vertex as a source or destination.

*  Run time: O(|E|).

*  Note that the total time for removing all |V| vertices in the

*  graph is also O(|E|) and not O(|V||E|). *)

valremove_vertex : graph -> vertex -> unit

(* add_edge (src, dst, w) adds an edge from src vertex to dst

*  vertex with weight w.

*  Run time: O(1). *)

valadd_edge : vertex * vertex * int -> unit

(* remove_edge (src, dst) removes the edge from src vertex to

*  dst vertex, and has no effect if the edge does not exist.

*  Run time: O(|E|). *)

valremove_edge : vertex * vertex -> unit (* Creates and returns a copy of the graph. * Run time: O(|V|+|E|). *)

val copy : graph -> graph

Note that the create function creates and returns an empty graph.

The add_vertex function takes a graph as argument, adds a new singleton vertex to that graph (a vertex with no edges starting or ending at that vertex), and returns the new vertex. The function add_edge takes two vertices and a weight and joins the vertices together by an edge. These are all O(1) time operations. The abstraction also provides operations for getting the list of vertices and edges of a graph, as well as the list of outgoing edges from a given vertex. There is also a functionincoming_ref which returns a list of reversed edges, by taking all the incoming edges for a given vertex and turning them into edges that go in the opposite direction. This function is useful for exploring the back-edges in a graph (i.e., exploring the reversed graph where all the edge directions are swapped). The Graph module in graph.ml implements this signature using adjacency lists of vertices, where both the outgoing edge list and the incoming edge for each vertex are explicitly represented. That is, each edge is stored twice, once at its source vertex and once at its destination vertex. This makes it easy to traverse the edges of the graph in reverse, which is useful for things like computing connected components (described below). In that implementation, a graph is represented as a pair consisting of the number of vertices and a list of vertices. A vertex is represented as a triple of a unique integer id, an outgoing list, and an incoming list. The outgoing list is a list of pairs of destination vertex and weight. The incoming vertex list is a list of pairs of source vertex and weight. Note that as each edge is stored twice, in the incoming list of its destination and the outgoing list of its source, the weight must be consistent in the two lists. In that implementation, an edge is a triple of a source vertex, destination vertex and weight, and is constructed on the fly as needed from the vertex out lists rather than being explicitly stored in the data structure.