Gauss's law and its applications

Gauss's law and its applications

Electric flux

Consider a closed surface S in a non?uniform electric field .

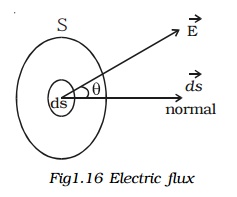
Consider a very small area ds on this surface. The direction of ds is drawn normal to the surface outward. The electric field over ds is supposed to be a constant Vector(E).  Vector(E) and Vector(ds) make an angle ? with each other.

The electric flux is defined as the total number of electric lines of force, crossing through the given area. The electric flux d? through the area ds is,

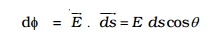
The total flux through the closed surface S is obtained by integrating the above equation over the surface.

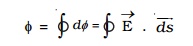
 The circle on the integral indicates that, the integration is to be taken over the closed surface. The electric flux is a scalar quantity.

Its unit is N m2 C-1

1. Gauss's law

The law relates the flux through any closed surface and the net charge enclosed within the surface. The law states that the total flux of the electric field E over any closed surface is equal to 1/εo times the net charge enclosed by the surface.

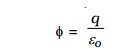
This closed imaginary surface is called Gaussian surface. Gauss's law tells us that the flux of E through a closed surface S depends only on the value of net charge inside the surface and not on the location of the charges. Charges outside the surface will not contribute to flux.

2. Applications of Gauss's Law

i. Electric field due to an infinite long straight charged wire

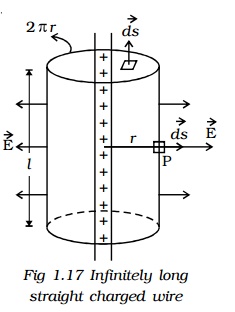
Consider an uniformly charged wire of infinite length having a constant linear charge density λ (charge per unit length). Let P be a point at a distance r from the wire (Fig. 1.17) and E be the electric field at the point P. A cylinder of length l, radius r, closed at each end by plane caps normal to the axis is chosen as Gaussian surface. Consider a very small area ds on the Gaussian surface.

By symmetry, the magnitude of the electric field will be the same at all points on the curved surface of the cylinder and directed radially outward.

The direction of electric field E is radially outward, if line charge is positive and inward, if the line charge is negative.

ii. Electric field due to an infinite charged plane sheet

Consider an infinite plane sheet of charge with surface charge density σ.. Let P be a point at a distance r from the sheet (Fig. 1.18) and E be the electric field at P. Consider a Gaussian surface in the form of cylinder of cross? sectional area A and length 2r perpendicular to the sheet of charge.

By symmetry, the electric field is at right angles to the end caps and away from the plane. Its magnitude is the same at P and at the other cap at P'.

Therefore, the total flux through the closed surface is given by

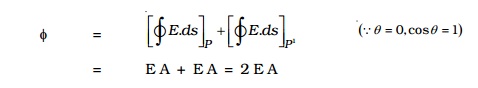
If σ is the charge per unit area in the plane sheet, then the net positive charge q within the Gaussian surface is, q = σA

Using Gauss's law,

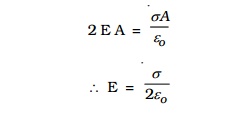
iii. Electric field due to two parallel charged sheets

Consider two plane parallel infinite sheets with equal and opposite charge densities +σ. and -σ. as shown in Fig 1.19. The magnitude of electric field on either side of a plane sheet of charge is E = σ./2εo and acts perpendicular to the sheet, directed outward (if the charge is positive) or inward (if the charge is negative).

(i) When the point P1 is in between the sheets, the field due to two sheets will be equal in magnitude and in the same direction. The resultant field at P1 is,

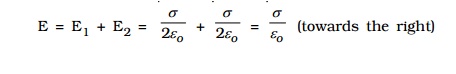
(ii) At a point P2 outside the sheets, the electric field will be equal in magnitude and opposite in direction. The resultant field at P2 is,

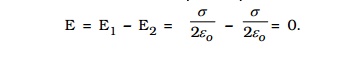
iv. Electric field due to uniformly charged spherical shell

Case (i) At a point outside the shell.

Consider a charged shell of radius R (Fig 1.20a). Let P be a point outside the shell, at a distance r from the centre O.

Let us construct a Gaussian surface with r as radius. The electric field E is normal to the surface.

The flux crossing the Gaussian sphere normally in an outward direction is,

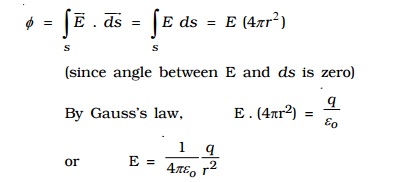
It can be seen from the equation that, the electric field at a point outside the shell will be the same as if the total charge on the shell is concentrated at its centre.

Case (ii) At a point on the surface.

The electric field E for the points on the surface of charged spherical shell is,

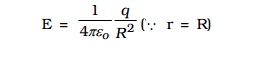
Case (iii) At a point inside the shell.

Consider a point P' inside the shell at a distance r' from the centre of the shell. Let us construct a Gaussian surface with radius r'.

The total flux crossing the Gaussian sphere normally in an outward direction is

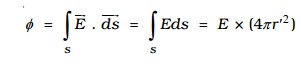
since there is no charge enclosed by the gaussian surface, according to Gauss's Law

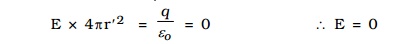
(i.e) the field due to a uniformly charged thin shell is zero at all points inside the shell.

v. Electrostatic shielding

It is the process of isolating a certain region of space from external field. It is based on the fact that electric field inside a conductor is zero.

During a thunder accompanied by lightning, it is safer to sit inside a bus than in open ground or under a tree. The metal body of the bus provides electrostatic shielding, where the electric field is zero. During lightning the electric discharge passes through the body of the bus.