Exterior Angles

Exterior Angles

We know that any triangle is made up of three vertices, three sides and three angles. Now observe the triangle given in Fig. 4.9

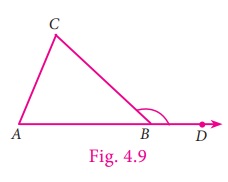
In ∆ABC, the side AB is extended to D. Observe ∠CBD side which is formed by the BC and BD. ∠CBD is known as the exterior angle of  ∆ABC at B.

We can observe that, ∠ABC and ∠CBD are adjacent and they form a linear pair.

Besides, the other two angles namely, ∠CAB and ∠ACB are non-adjacent angles to ∠CBD. They are called interior opposite angles of ∠ CBD.

Think

Can CB be extended to F to get another exterior angle of ∆ABC at B?

Note

In ∆ABC, we can also extend the sides BC to E and CA to F to form exterior angles at C and A.

Exterior Angle Properties of a Triangle

Activity

To understand exeterior angle properties of a triangle list all the exterior angles of triangles that are shown below.

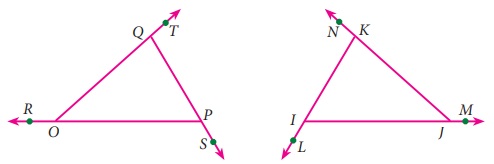
Measure and express each exterior angle as a sum of its interior opposite angles and complete the table.

From the above activity we observe that an exterior angle of a triangle is equal to the sum of its interior opposite angles.

Now we prove this result in a formal method.

Proof

In  ∆ABC, consider, the angles at A, B and C as a, b and c respectively and take exterior angles at A, B and C as x, y and z respectively.

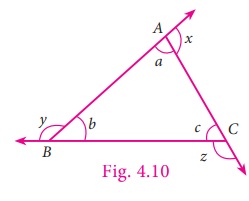
We are going to prove x=b+c,  y=a+c and z=a+b

a + x = 180° [linear pair of angles are supplementary]

This gives, x = 180° – a … (1)

Now, a + b + c = 180° [Sum of 3 angles in a triangle is 180°]

This gives, b + c = 180° – a …(2)

From (1) and (2),

x and b + c both are equal.

Therefore, x = b + c.

In the same way, we can prove the result for other exterior angles.

Now we are going to learn one more result on the exterior angle of a triangle for which we do the following activity.

Activity

Imagine a person standing in one of the vertices (corners) and walking along the boundary of the triangle until he reaches the starting point. At each of the vertex of the triangle he would turn an angle equal to the exterior angle at that vertex. Hence after the complete journey around the triangle he would have turned through an angle equal to one complete revolution, that is 360°.

We prove this result as below.

Since the angles on a straight line is 180º ,

We have a + x = 180° [linear pair of angles are supplementary]

                     x = 180° – a

Similarly,     y = 180° –b

             and z = 180° – c

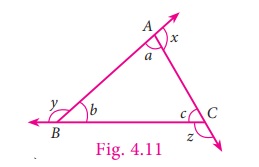
Therefore,    x + y + z = (180° – a) + (180° – b) + (180° – c)

                                    = 540 – (a + b + c)

                                    =540°–180°  [sum of all three angles of a triangle is 180°]

                                    =360°

Hence, the sum of all exterior angles of a triangle is 360°.

Therefore, the properties of exterior angle gives us the following two results.

(i) An exterior angle of a triangle is equal to the sum of its interior opposite angles.

(ii) The sum of exterior angles of a triangle is 360º .

Example 4.5

In ∆PQR , find the exterior angle, ∠SRQ .

Solution

Let, ∠SRQ = x

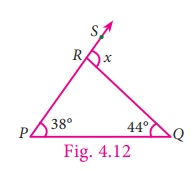
Exterior angle = sum of two interior opposite angles

x= 38° + 44° = 82°

Example 4.6

In ∆LMN , LM is extended to O. If ∠L = 62° and ∠N = 31°, find ∠NMO .

Solution

Let, ∠NMO = y

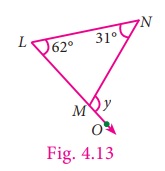
Exterior angle = sum of two interior opposite angles

y= 62° +31°

= 93°

Example 4.7

In the ∆ABC shown in the figure, find the angel z.

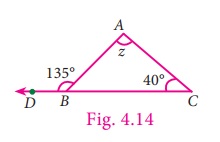
Solution

Exterior angle = sum of two interior opposite angles

135° = z + 40°

Subtract 40° on both sides

135° − 40° = z + 40° − 40°

z= 95°

Example 4.8

In the given isoceles triangle IJK (Fig. 4.15), if ∠IKL = 128°, find the value of x.

Solution

Exterior angle = sum of two interior opposite angles

128° = x + x

128= 2x

128/2 = 2x/2  [on both sides, divide by 2]

x= 64°

Example 4.9

With the given data in the Fig. 4.16, find ∠UWY . What do you infer about ∠XWV ?

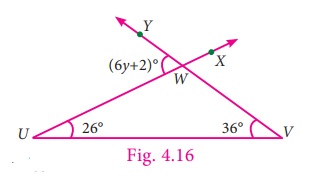
Solution

Exterior angle = sum of two interior opposite angles

 6 y + 2 = 26° + 36°

6 y + 2 = 62°

Subtract 2 from both sides

6 y = 62 – 2

6 y = 60°

6y/6 = 60/6      [on both sides, divide by 6]

y=10º

∠UWY = 6y + 2 = 6(10) + 2 = 62º .

We can conclude that ∠XWV = ∠UWY , because they are vertically opposite angles as well as exterior angles.