Exercise 4.2 (Congruency of Triangles)

Exercise 4.2

1. Given that ∆ABC ≡ ∆DEF 

(i) List all the corresponding congruent sides 

Corresponding sides: AB, DE; BC, EF; AC, DF.

(ii) List all the corresponding congruent angles.

Corresponding angles: ∠ABC, ∠DEF; ∠BCA, ∠EFD; ∠CAB, ∠FDE.

2. If the given two triangles are congruent, then identify all the corresponding sides and also write the congruent angles.

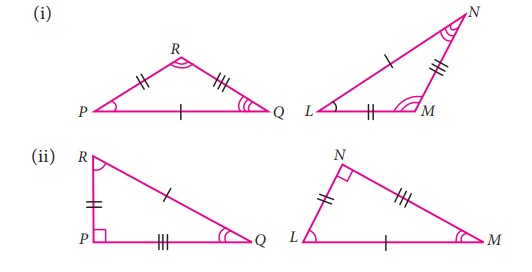
Solution:

(i) Corresponding sides:

∠RPQ = ∠NLM; ∠PQR = ∠LNM; ∠PRQ = ∠LMN;

(ii) Determine congruent angles

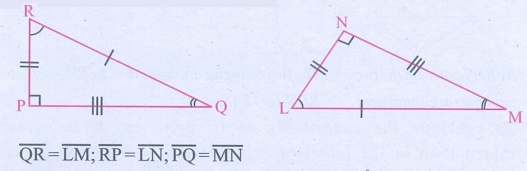
∠PQR=∠LMN; ∠QRP = ∠MLN; ∠RPQ = ∠LNM

3. If the given triangles ∆ABC and ∆EFG are congruent, determine whether the given pair of sides and angles are corresponding sides or corresponding angles or not.

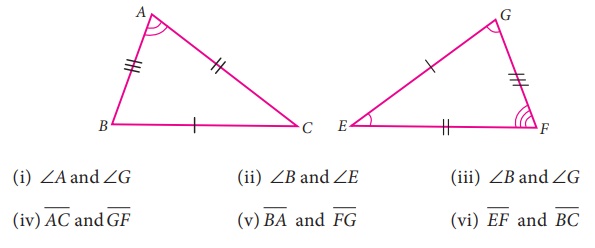
Solution:

(i) ∠A and ∠G

Not corresponding angles

(ii) ∠B and ∠E

Not corresponding angles

(iii) ∠B and ∠G

corresponding angles

(iv) AC̅ and GF̅

Not corresponding angles

(v) BA̅ and FG̅

corresponding angles

(vi) EF̅ and BC̅

Not corresponding angles

4. State whether the two triangles are congruent or not. Justify your answer.

Solution:

(i) By SAS criterion the two triangles are congruent

(ii) By SSS criterion the two triangles are congruent

(iii) By AAA criterion the two triangles are congruent

(iv) By RHS criterion the two triangles are congruent

(v) The two triangles are congruent by SSS (or) RHS (or) SAS.

5. To conclude the congruency of triangles, mark the required information in the following figures with reference to the given congruency criterion.

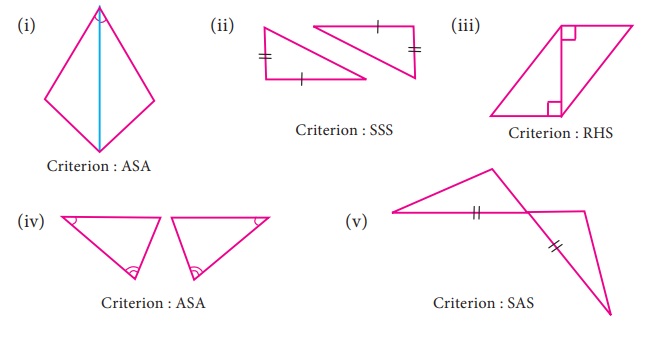
Solution:

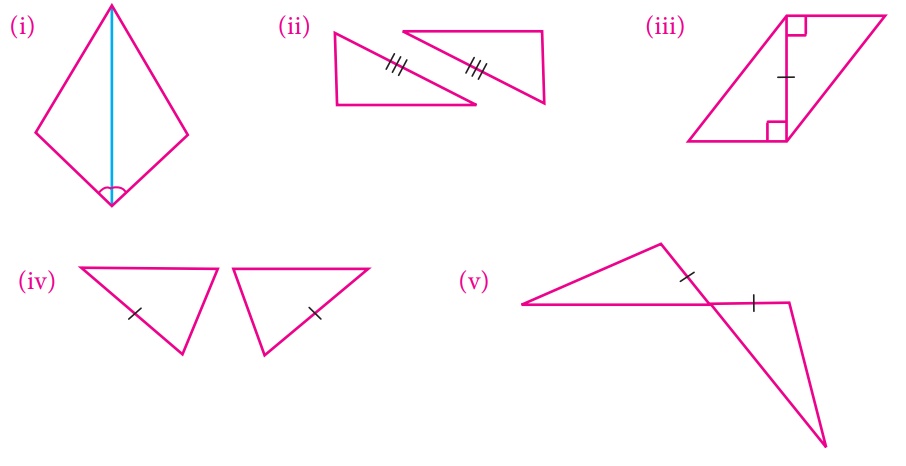
6. For each pair of triangles state the criterion that can be used to determine the congruency?

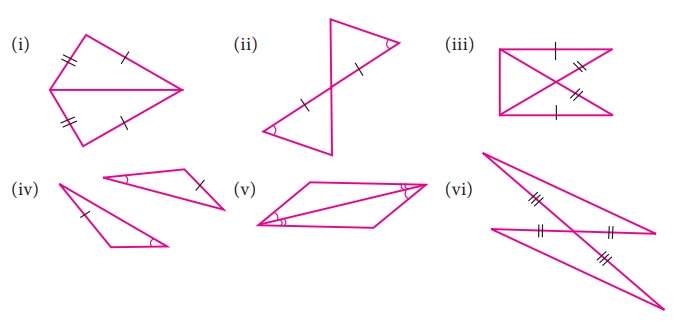
Answer:

(i) SSS criterion

(ii) ASA criterion

(iii) RHS criterion

(iv) ASA criterion

(v) ASA criterion

(vi) SAS criterion

7. I. Construct a triangle XYZ with the given conditions.

(i) XY = 6.4 cm, ZY = 7.7 cm and XZ = 5 cm

Solution:

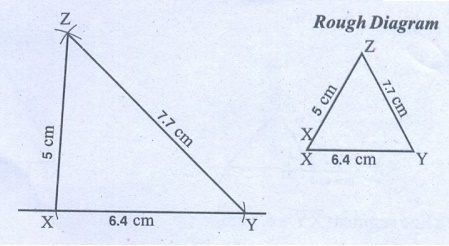
Steps:

1. Draw a line segment X̅ Ȳ = 6.4 cm.

2. With X as centre, draw an arc of radius 5 cm above the line XY.

3. With Y as centre, draw another arc of radius 7.7 cm to intersect the previous arc at Z.

4. Join XZ and YZ.

Now XYZ is the required triangle. 

(ii) An equilateral triangle of side 7.5 cm

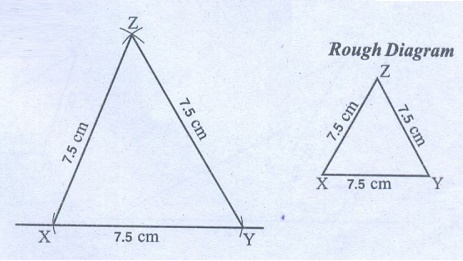
Steps:

1. Draw a line segment X̅Ȳ = 7.5 cm.

2. With X as centre, draw an arc of radius 7.5 cm above the line XY another.

3. With Y as centre draw another arc of radius 7.5 cm to interest the previous arc at Z.

4. Join XZ and YZ.

Now XYZ is the required triangle.

(iii) An isosceles triangle with equal sides 4.6 cm and third side 6.5 cm

Steps:

1. Draw a line segment X̅ Ȳ = 6.5 cm.

2. With X as centre, draw an arc of radius 4.6 cm.

3. With Y as centre draw another arc of radius 4.6 cm to intersect the previous arc at Z.

4. Join XZ and YZ.

Now XYZ is the required triangle.

II. Construct a triangle ABC with given conditions.

(i) AB = 7 cm, AC = 6.5 cm and ∠ A = 120°.

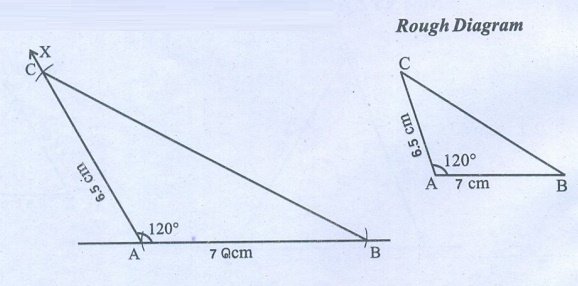
Steps:

1. Draw a line segment AB = 7cm.

2. At A, draw a ray AX making an angle of 120° with AB.

3. With A as centre, draw an arc of radius 6.5 cm to cut the ray AX at C.

4. Join BC.

Now ABC is the required triangle.

(ii) BC = 8 cm, AC = 6 cm and ∠ C = 40°.

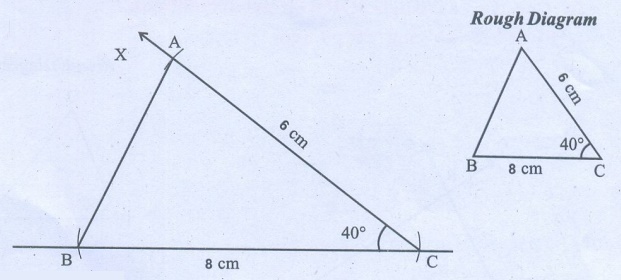
Steps:

1. Draw a line segment B̅C̅ = 8 cm.

2. At C draw a ray CX making an angle of radius.

3. With C as centre draw an arc of radius 6 cm.

4. Join AB.

Now ABC is the required triangle,

(iii) An isosceles obtuse triangle with equal sides 5 cm

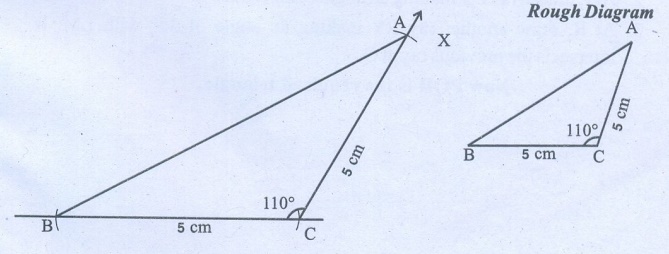
Steps:  

1. Draw a line segment A̅B̅ = 5 cm.

2. At B, draw a ray BX making an angle of 110° with AB.

3. With B as centre, draw an arc of radius 5 cm to cut the ray BX at C.

4. Join AC.

Now ABC is the required triangle.

III. Construct a triangle PQR with given conditions.

(i) ∠ P = 60°, ∠ R = 35° and PR = 7.8 cm

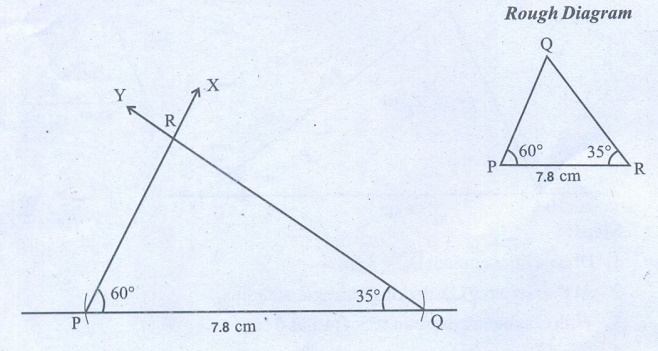
Steps:

1. Draw a line segment P̅R̅ = 7.8 cm.

2. At P, draw a ray PX making an angle of 60° with PR.

3. At R, draw another ray RY making an angle of 35° with LM. It intersects the previous ray at Q.

Now PQR is the required triangle. 

(ii) ∠ P = 115°, ∠ Q = 40° and PQ = 6 cm

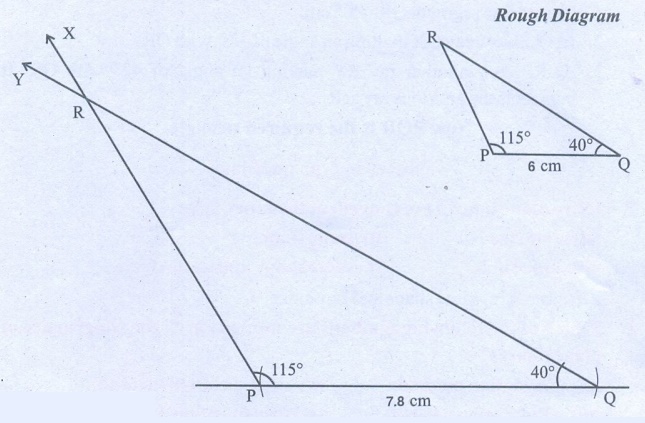
Steps:

1. Draw a line segment P̅Q̅ = 6 cm.

2. At P, draw a ray PX making an angle of 115° with PQ.

3. At Q, draw another ray QY making an angle of 40° with PQ. It intersects the previous ray at R.

Now PQR is the required triangle. 

(iii) ∠ Q = 90°, ∠ R = 42° and QR = 5.5 cm

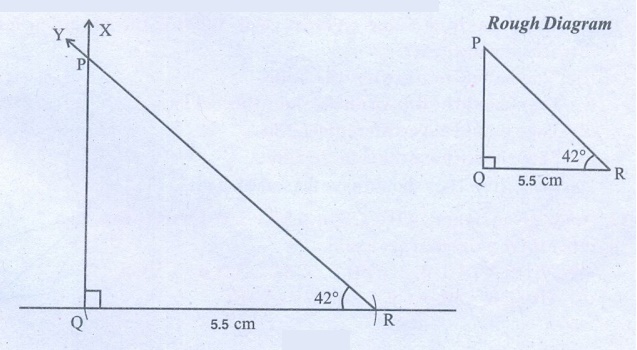
Steps:

1. Draw a line segment QR = 5.5 cm.

2. At Q, draw a ray QX making an angle of 90° with QR.

3. At R, draw another ray RY making an angle of 42° with QR. It intersects the previous ray at R

Now PQR is the required triangle.

Objective type questions

8. If two plane figures are congruent then they have

(i) same size

(ii) same shape

(iii) same angle

(iv) same shape and same size

Answer : (iv) same shape and same size

9. Which of the following methods are used to check the congruence of plane figures?

 (i) translation method

 (ii) superposition method

 (iii) substitution method

(iv) transposition method

Answer : (ii) superposition method

10. Which of the following rule is not sufficient to verify the congruency of two triangles.

(i) SSS rule

(ii) SAS rule

(iii) SSA rule

(iv) ASA rule

Answer : (iii) SSA rule

11. Two students drew a line segment each. What is the condition for them to be congruent?

(i) They should be drawn with a scale.

(ii) They should be drawn on the same sheet of paper.

(iii) They should have different lengths.

(iv) They should have the same length.

Answer : (iv) They should have the same length

12. In the given figure, AD=CD and AB=CB. Identify the other three pairs that are equal.

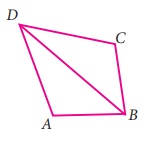
(i) ∠ADB = ∠CDB, ∠ABD = ∠CBD, BD = BD

(ii) AD=AB, DC=CB, BD=BD

(iii) AB=CD, AD=BC, BD=BD

 (iv) ∠ADB = ∠CDB, ∠ABD = ∠CBD, ∠DAB = ∠DBC

Answer: (i) ∠ADB = ∠CDB, ∠ABD = ∠CBD, ∠DAB = ∠DCB

13. In ∆ABC and ∆PQR, ∠ A=50°= ∠ P, PQ=AB, and PR=AC. By which property ∆ABC and ∆PQR are congruent?

(i) SSS property

(ii) SAS property

(iii) ASA property

(iv) RHS property

Answer : (ii) SAS property

ANSWERS:

Exercise 4.2

1. Corresponding sides : AB, DE; BC, EF; AC, DF

Corresponding angles : ∠ ABC, ∠ DEF; ∠ BCA, ∠ EFD; ∠ CAB, ∠ FDE

2. (i)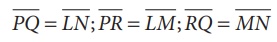 

∠RPQ = ∠NLM; ∠PQR = ∠LNM; ∠PRQ = ∠LMN

 (ii)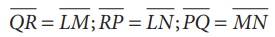 

 ∠PQR = ∠LMN; ∠QRP = ∠MLN; ∠RPQ = ∠LNM

3. (i) Not corresponding angles (ii) Not corresponding angles  (iii) corresponding angles (iv) Not corresponding sides  (v) corresponding sides (vi) Not corresponding sides

4. (i) congruent triangles by SAS (ii) congruent triangles by SSS  (iii) congruent triangles by AAA (iv) congruent triangles by RHS  (v) congruent triangles by SSS (or) RHS (or) SAS

5. 

6. (i) SSS (ii) ASA (iii) RHS   (iv) ASA (v) ASA (vi) SAS

Objective type questions

8. (iv) same shape and same size

9. (ii) superposition method

10. (iii) SSA rule

11. (iv) They should have the same length

12. (i) ∠ADB = ∠CDB; ∠ABD = ∠CBD; BD = BD

13. (ii) SAS property