Exercise 4.3

Exercise 4.3

Miscellaneous Practice problems

1. In an isosceles triangle one angle is 76°. If the other two angles are equal find them.

Solution: 

In an isosceles triangle one angle = 76°

Sum of three angles = 180°

The other two equal angles = 180° – 76°

 = 104°

One angle = 104/2 = 52°

The other two equal angles are 52°, 52°.

2. If two angles of a triangle are 46° each, how can you classify the triangle?

Solution: 

If two angles are equal Corresponding two sides also equal. So it is an isosceles triangle.

3. If one angle of a triangle is equal to the sum of the other two angles, find the type of the triangle.

Solution: 

One angle = Sum of two angles

90° = 45°+ 45°

So, the triangle is the right angled triangle.

4. If the exterior angle of a triangle is 140° and its interior opposite angles are equal, find all the interior angles of the triangle.

Solution: 

The exterior angle of a triangle = 140°

The exterior angle = Sum of two interior opposite angles. The interior opposite angles are equal. 

The sum of two interior oppositeangles = 140°

One angle = 140 / 2 = 70^o

Third angle = 180° – 140° = 40°

The three angles = 70°, 70°, 40°

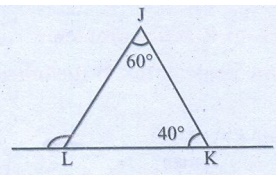
5. In ∆JKL, if ∠J = 60° and ∠ K = 40°, then find the value of exterior angle formed by extending the side KL.

Solution: 

The exterior angle = Sum of two interior opposite angles.

The exterior angle ∠L = 60° + 40° = 100°

6. Find the value of ‘x’ in the given figure.

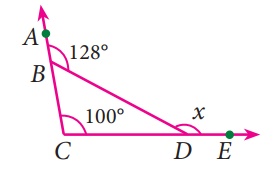
Solution: 

The exterior angle ∠ABD = 128°

The exterior angle = Sum of two interior opposite angles.

128° = ∠BCD + ∠BDC

100° + ∠BDC = 128°

∠BDC = 128° – 100° = 28°

The inner angle ∠BDC = 28°

∠BDC + x = 180° (Linear angles)

28° + x =180°

 x = 180° – 28° = 152°

 x = 152°

7. If ∆MNO ≡ ∆ DEF, ∠ M = 60° and ∠ E = 45° then find the value of ∠ O.

Solution: 

∆MN0 ≅ ∆DEF

∠M = ∠D, ∠N = ∠E, ∠O = ∠F

∠E = 45°

∠N = 45°

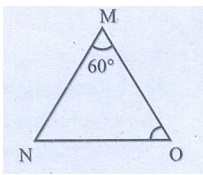
Sum of three angles of a triangle = 180°

∠M + ∠N + ∠O = 180°

60° + 45°+ ∠O = 180°

105° + ∠O = 180°

∠O = 180° – 105° = 75°

∠O = 75°

8. In the given figure ray AZ bisects ∠ BAD and ∠ DCB, prove that (i) ∆BAC ≡ ∆DAC (ii) AB = AD.

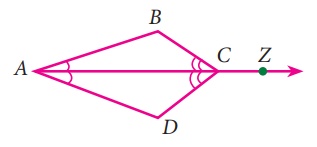
Solution: 

From the given figure,

In ∆ BAC and ∆ DAC,

The ray AZ is the angle bisector of ∠A and ∠C

 ∴ ∠BAC = ∠DAC

 ∠BCA = ∠DCA

AC is common By

ASA criterion

 ∆ BAC ≅ ∆ DAC

∆BAC and ∆ DAC are congruent triangles, then their corresponding parts are congruent. ∴ AB = AD.

9. In the given figure FG = FI and H is midpoint of GI, prove that ∆FGH ≡ ∆FHI

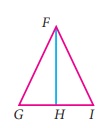
Solution: 

From the figure, In ∆FGH and ∆FHI,

H is the mid point of GI.

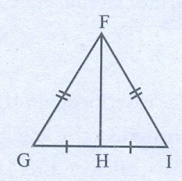
So, GH = HI

FG = FI (Given)

FH is common

By SSS criterion, ∆FGH ≅ ∆FHI

10. Using the given figure, prove that the triangles are congruent. Can you conclude that AC is parallel to DE.

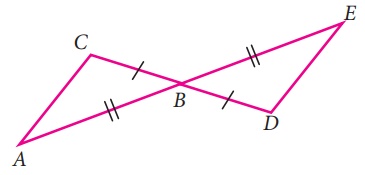
Solution: 

From the figure, In ∆ ABC and ∆ BDE,

AB = BE

BC = BD 

∠ABC = ∠DBE (Vertically opposite angles)

By SAS criterion,

∆ABC ≅   ∆BDE

So, AC = DE and AC | | DE

Challenge Problems

11. In given figure BD = BC, find the  value of x.

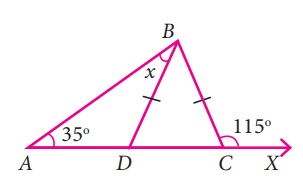
Solution: 

In ∆ ABC, Exterior angle ∠C = 115°

∠BCD + 115° = 180° (Linear angles)

∠BCD = 180°–115° = 65°

BD = BC (Given)

So, ∠BCD = ∠BDC

∠BCD = 65°

So, ∠BDC = 65°

The exterior angle of ∠BAD is ∆BDC.

The exterior angle ∠BDC = The sum of two interior opposite angles.

65° = 35° + x

x = 65°– 35° = 30°

12. In the given figure find the value of x.

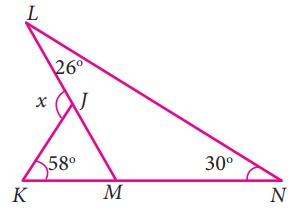
Solution: 

From the figure,

The exterior angle of ∆LMN is ∠KML.

So the exterior angle ∠KML = Sum of two interior opposite angles.

 = ∠MLN + ∠MNL

 = 26° + 30° = 56°

The exterior angle of ∆KMJ is ∠KJL.

So, the exterior angle ∠KJL = Sum of two interior opposite angles,

x = ∠JKM + ∠KMJ

 = 58° + 56° = 114°

x = 114°

13. In the given figure find the values of  x and y.

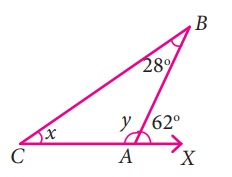
Solution: 

From the figure,

The exterior angle ∠BAX = Sum of two interior opposite angles.

62°. = ∠ABC + ∠ACB

62° = 28° + x

x = 62° – 28 = 34^o

x = 34°

∠CAB + ∠BAX = 180° (Linear angles)

y + 62° = 180°

y = 180°– 62° = 118°

y = 118°

x = 34°

y = 118°

14. In ∆DEF, ∠F = 48°, ∠E = 68° and bisector of ∠D meets FE at G. Find ∠FGD.

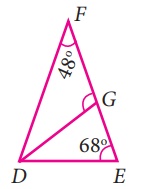
Solution: 

From the figure,

In ∆DEF,

∠D + ∠E + ∠F = 180° (Sum of three angles of a triangle)

∠D + 68° + 48° = 180°

∠D +116° = 180°

∠D = 180° – 116° = 64°

Angle bisector of ∠D is DG,

So, ∠FDG = ∠EDG ………… (1)

∠FDG + ∠EDG = 64°

From equation ………. (1)

∠EDG + ∠EDG = 64°

2 ∠EDG = 64°

∠EDG = 32°

The exterior angle ∠FGD = Sum of two interior opposite angles.

 = ∠DEG + ∠EDG

∠FGD = 68° + 32° = 100°

∠FGD = 100° 

15. In the figure find the value of x.

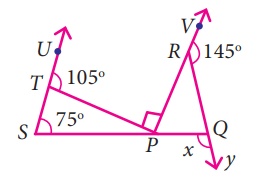
Solution: 

From the figure,

The exterior angle ∠UTP = Sum of two interior opposite angles.

105° = ∠TSP + ∠TPS

105° = 75° + ∠TPS

∠TPS = 105° – 75° = 30°

∠TPS + ∠TPR + ∠RPQ = 180° (Linear angles)

30° + 90° + ∠RPQ = 180°

120° + ∠RPQ = 180°

∠RPQ =180° – 120° = 60°

∠RPQ = 60^o

∠VRQ + ∠QRP = 180^o (Linear angles)

145^o + ∠QRP = 180°

∠QRP = 180 – 145° = 35°

The exterior angle ∠PQY = Sum of two interior opposite angles.

∠QRP + ∠RPQ

x = 60^o + 35^o = 95°

x = 95°

16. From the given figure find the value of y

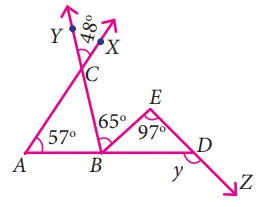
Solution: 

From the figure,

∠YCX =48°

∠YCX = ∠ACB (Vertically opposite angles)

∴ ∠ACB = 48°

The exterior angle ∠CBD = Sum of two interior opposite angles.

 = ∠BAC + ∠ACB = 57° + 48° = 105°

∠CBD = ∠CBE + ∠EBD

105° = 65° + ∠EBD

∠EBD = 105° – 65° = 40°

The exterior angle ∠BDZ = The two interior opposite angles.

∠BED + ∠EBD

y = 97° + 40° = 137°

y = 137° 

ANSWERS:

Exercise 4.3

1. 52°, 52°

2. Isoceles triangle

3. Right angled triangle

4. 40°, 70°, 70°

5. 100°

 6. 152°

7. ∠O = 75º

10. (SAS), ∆CAB ≅ ∆EBD ; AC || DE

Challenge problems

11. x = 30º

 12. x = 114º

13. x = 34º; y = 118º

14. 100°

15. 95°

16. y = 137º