Application of Angle Sum Property of Triangle

Application of Angle Sum Property of Triangle

We are familiar with the angle sum property of a triangle which can be stated as the sum of all angles in a triangle is 180°. We can verify this by doing the following activity.

Activity

Draw any triangle and colour the angles. Check the property as shown below:

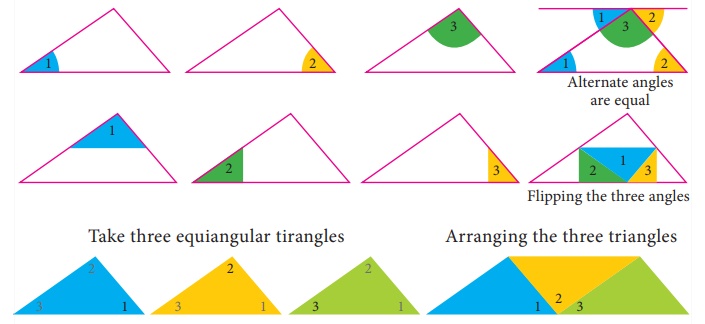
From the above we have verified that the sum of three angles of any triangle is 180°

From the above activity, we get the result as, the sum of three angles of any triangle is 180°.

Now we prove the result in a formal method.

Given: A triangle ABC, where ∠A = x , ∠B = y and ∠C = z .

Now let us prove, x + y + z = 180°.

To show this we need to extend BC to D and draw a line CE, parallel to AB.

Now CE makes two angles, ∠ACE and ∠ECD .

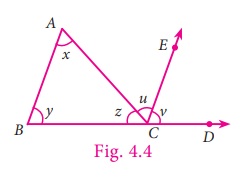
Let it be u and v respectively.

Now z, u, v are the angles formed at a point on a straight line.

Therefore z + u + v = 180°   . ... (1)

Since AB and CE are parallel and DB is a transversal,

v = y (corresponding angles).

Again AB and CE are parallel lines and AC is a transversal,

u = x (alternate angles). Also z + u + v = 180° [by (1)]

Hence, by replacing u as x and v as y, we get x + y + z = 180°.

Hence the sum of all three angles in a triangle is 180°.

Example 4.1

Can the following angles form a triangle?

(i) 80°, 70°, 50°

(ii) 56°, 64°, 60°

Solution

(i) Given angles 80°, 70°, 50°

Sum of the angles = 80°+70°+ 50° = 200° ≠ 180°

The given angles cannot form a triangle.

(ii) Given angles 56°, 64°, 60°

Sum of the angles = 56°+ 64°+ 60° = 180°

The given angles can form a triangle.

Example 4.2

Find the measure of the missing angle in the given triangle ABC.

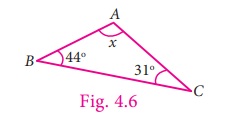
Solution

Let ∠A = x

We know that,

∠A+ ∠B+∠C=180° (angle sum property)

x + 44° + 31° = 180°

x + 75° = 180°

x = 180°– 75°

x = 105°

Example 4.3

In ∆STU, if SU = UT, ∠SUT = 70°, ∠STU = x, find the value of x.

Solution

Given, ∠SUT = 70°

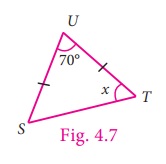
∠UST = ∠STU = x [Angles opposite to equal sides]

∠SUT + ∠UST +∠STU = 180°

70° + x + x = 180°

70° + 2x = 180°

2x = 180°– 70°

2x = 110°

x = 110º / 2 = 55°

Example 4.4

If two angles of a triangle having measures 65° and 35°, find the measure of the third angle.

Solution

Given angles are 65° and 35°.

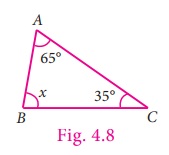
Let the third angle be x

65° + 35°+ x = 180°

100° + x = 180°

x= 180°–100°

x = 80°