Exercise 4.1 (angles of triangle)

Exercise 4.1

1. Can 30°, 60° and 90° be the angles of a triangle?

Solution: 

Given angles 30°, 60°, 90°

Sum of the angles = 30°+ 60°+ 90° = 180°

The given angles can form a triangle.

2. Can you draw a triangle with 25°, 65° and 80° as angles?

Solution: 

Given angles 25°, 65°, 80°

Sum of the angles = 25°+ 65°+ 80° = 170° ≠ 180°

The given angles can not form a triangle.

3. In each of the following triangles, find the value of x.

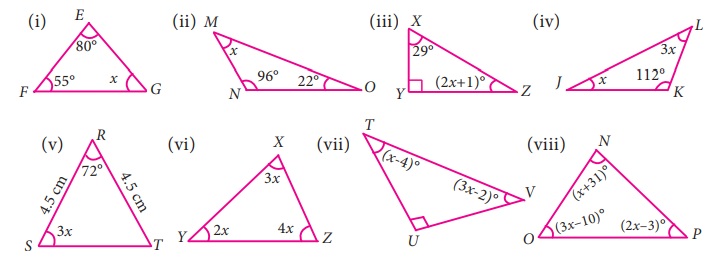
Solution: 

i) ∠E + ∠F + ∠G = 180°

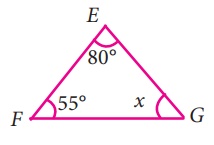
80° + 55° + x =180°

135° + x =180°

x = 180° – 135° = 45°

x = 45°

ii) ∠M + ∠N + ∠O = 180°

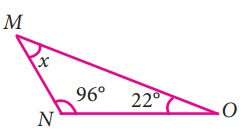
x + 96° + 22° =180°

x + 118° =180°

x =180° – 118^o = 62^o

x = 62°

iii) ∠X + ∠Y + ∠Z =180°

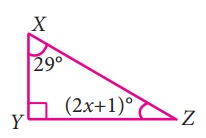
29° + 90° + 2x + l = 180°

 120° + 2x =180°

2x =180° – 120^o = 60^o

x = 30°

iv) ∠L + ∠J + ∠K = 180°

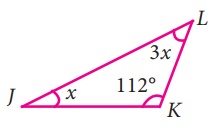
3x + x +112° = 180°

4x + 112° = 180°

4x = 180° – 112° = 68°

x = 68 / 4 = 17^o

x=17°

v) ∠S + ∠R + ∠T = 180°

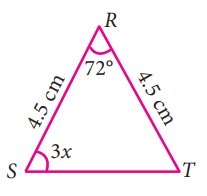
Side SR = Side RT

So, ∠S = ∠T

∠S = 3x ∴ ∠T = 3x

 ∠S + ∠R + ∠T = 3x + 3x + 72^o = 180^o

 = 6x + 72^o = 180^o

 = 6x = 180°–72° = 108°

 x = 180^o /6 = 18°

x = 18°

vi) ∠X + ∠Y + ∠Z = 180^o

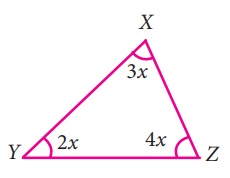
3x + 2x + 4x = 180^o

9x = 180^o

 X = 108 / 9 = 20^o

x = 20°

vii) ∠U + ∠V + ∠T = 180°

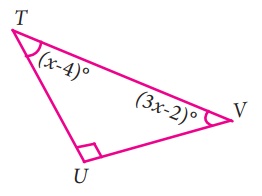
90° + 3x –2 + x –4 = 180°

84° + 4x = 180°

4x = 180° – 84^o = 96^o

 x = 96 / 4 = 24^o

x = 24^o

viii) ∠N + ∠O + ∠P = 180°

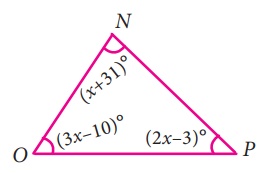
x + 31+ 3x –10 + 2x –3 = 180°

6x + 18 = 180°

6x = 180° – 18° = 162°

 x = 162/6  = 27^o

 x = 27^o

4. Two line segments  and  intersect at O. Joining and   we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠ A and ∠ B.

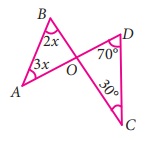
Solution: 

From the figure,

In ∆ OCD,

∠COD + ∠OCD + ∠ODC = 180^o

∠COD + 30° + 70° = 180^o

∠COD + 100^o = 180^o

∠COD = 180^o – 100^o = 80°

∠COD = 80°

∠COD = ∠AOB = 80° (Vertically opposite angles)

 In ∆ AOB,

∠OAB + ∠ABO + ∠AOB = 180°

3x + 2x + 80° = 180°

5x = 180° – 80° = 100°

 x = 100 / 5 = 20°

x = 20° 

∠B = 2x = 2 x 20° = 40°

∠A = 3x = 3 x 20° = 60°

∠A = 60°, ∠B = 40°

5. Observe the figure and find the value of

∠A+∠N+∠G+∠L+∠E+∠S.

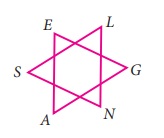
Solution: 

From the figure, ∆AGE and ∆SNL are equilateral triangles. So each angle is 60°.

So, ∠A + ∠N + ∠G + ∠L + ∠E + ∠S = 60° + 60° + 60° + 60° + 60° + 60°

= 360°

6. If the three angles of a triangle are in the ratio 3 : 5 : 4 , then find them.

Solution: 

Sum of the three angles in a triangle = 180°

The ratio of the three angles = 3:5:4

Let the three angles be 3x, 5x, 4x.

Sum of the three angles = 3x,5x,4x =180°

 12x =180°

  x = 180 / 2 =15°

 x = 15°

 3x = 3 × 15° = 45°

 5x = 5 × l5° = 75°

 4x = 4 × 15° = 60°

The three angles are 45°, 75°, 60°

7. In ∆RST , ∠S is 10° greater than ∠R and ∠T is 5° less than ∠S , find the three angles of the triangle.

Solution: 

In ∆ RST

∠S = ∠R + 10°

∠T = ∠S – 5°

= ∠R + 10° – 5°

∠T = ∠R + 5°

Sum ofthe three angles of a triangle = 180°

∠R + ∠S + ∠T = 180°

∠R + ∠R + 10° + ∠R + 5° = 180°

3∠R + 15^o = 180°

3∠R = 180° – 15^o = 165°

 ∠R = 165 / 3 = 55°

∠R = 55°

∠S = 55° + 10° = 65°

∠T= 55° + 5 = 60°

The three angles are 55°, 65°, 60°

8. In ∆ABC , if ∠B is 3 times ∠A and ∠C is 2 times ∠A , then find the angles.

Solution: 

In ∆ ABC

∠B = 3∠A

∠C = 2∠A

Sum of the three angles = 180°

∠A + ∠B + ∠C = 180°

∠A + 3∠A + 2∠A =180°

6∠A =180°

 ∠A = 180 / 6 = 30^o

∠A= 30°

∠B = 3∠A = 3 × 30° = 90°

∠C = 2∠A = 2 × 30° = 60°

The three angles are 30°, 60°, 90°

9. In ∆XYZ , if ∠X : ∠Z is 5 : 4 and ∠Y = 72°. Find ∠X and ∠Z

Solution: 

In ∆ XYZ , ∠Y = 72°

∠X : ∠Z = 5:4

Let ∠X = 5x, ∠Z = 4x

Sum of the three angles = 180°

5x + 4x + 72° = 180°

9x + 72° = 180° 

9x = 180° – 72° = 108°

 x = 108^o/9 = 12^o

∠X = 5x = 5 × 12 = 60°

∠X = 60°

∠Z = 4x = 4 × 12 = 48°

∠Z = 48°

∠X = 60° ; ∠Z = 48°

10. In a right angled triangle ABC, ∠B is right angle, ∠A is x + 1 and ∠C is 2x + 5 . Find ∠A and ∠C .

Solution: 

In right ∆ ABC,

∠B = 90°             ∠A = x + 1

∠A + ∠C = 90°   ∠C = 2x + 5

x + l + 2x + 5 = 90°

3x + 6 = 90°

3x = 90 – 6 = 84°

 x = 84 / 3 = 28^o

x = 28°

∠A = x + 1 = 28° + 1 = 29°

∠C = 2x + 5 = 2 × 28 + 5 = 56 + 5 = 61°

∠A = 29°

∠C = 61°

11. In a right angled triangle MNO, ∠N = 90°, MO is extended to P. If ∠NOP = 128°, find the other two angles of ∆MNO .

Solution: 

In right ∆ MNO,

∠N =90°

∠NOP =128°

∠MON + ∠NOP = 180° (linear angles)

∠MON + 128° =180°

∠MON = 180°– 128° = 52°

∠MON = 52°

∠MON + ∠NMO = 90°

52° + ∠NMO = 90°

∠NMO = 90° – 52° = 38°

The other two angles,

∠M = 38°

∠O = 52°

12. Find the value of x in each of the given triangles.

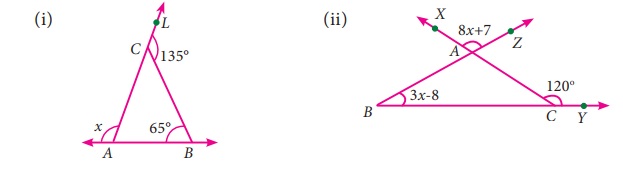
Solution: 

i) Exterior angle ∠BCL = Sum of two interior opposite angles

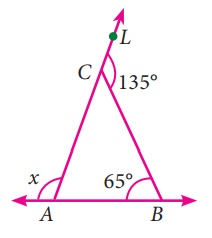
135° = 65° + ∠BAC

∠BAC = 135° – 65° = 70°

x + ∠BAC = 180° (Linear angles)

x + 70^o = 180°

x = 180° – 70° = 110°

x = 110°

ii) From the figure, ∠BAC = ∠XAZ = 8x + 7 (Vertically opposite angle)

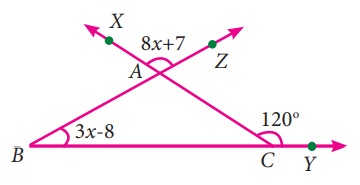
∠BAC = 8x + 7

Exterior angle ∠ACY = Sum of two interior opposite angles. 

120° = ∠BAC + ∠ABC

120° = 8x + 7 + 3x – 8

11x – 1 = 120

11 x = 120 + 1 = 121

 x = 121/ 11=11

x = 11°

13. In ∆LMN, MN is extended to O. If ∠MLN = 100 – x, ∠LMN = 2x and ∠LNO = 6x – 5, find the value of x.

Solution: 

Exterior angle ∠LNO = Sum of two interior opposite angles.

6x – 5 = 100 – x + 2x

6x – 5 = 100 + x

6x – x = 100 + 5

5x = 105

 x = 105 / 5 = 21°

x = 21°

14. Using the given figure find the value of x.

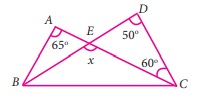
Solution: 

Exterior angle ∠BEC = Sum of two interior opposite angles.

x = ∠EDC + ∠ECD

x = 50° + 60° = 110°

x = 110°

x = 110°

15. Using the diagram find the value of x.

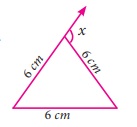
Solution: 

Angles of the equilateral triangle.

So, ∠A = ∠B = ∠C = 60°

Exterior angle x = Sum of two interior opposite angles 

x = ∠B + ∠C

x = 60° + 60° = 120°

x = 120°

x = 120°

Objective type questions

16. The angles of a triangle are in the ratio 2:3:4. Then the angles are

(i) 20, 30, 40

(ii) 40, 60, 80

 (iii) 80, 20, 80

(iv) 10, 15, 20

Answer : (ii) 40,60,80

17. One of the angles of a triangle is 65°. If the difference of the other two angles is 45°, then the two angles are

(i) 85°, 40°

(ii)70°, 25°

(iii) 80° , 35°

(iv) 80° , 135°

Answer : (iii) 80°, 35°

18. In the given figure, AB is parallel to CD. Then the value of b is

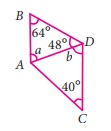
(i) 112°

 (ii) 68°

(iii) 102°

 (iv) 62°

Answer : (ii) 68°

19. In the given figure, which of the following statement is true?

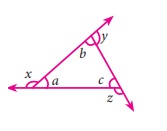
(i) x + y + z = 180°

(ii) x + y + z = a + b + c

(iii) x + y + z = 2(a + b + c)

(iv) x + y + z = 3(a + b + c)

Answer : (iii) x+y+z = 2(a+b + c)

20. An exterior angle of a triangle is 70° and two interior opposite angles are equal. Then measure of each of these angle will be

(i) 110°

(ii) 120°

(iii) 35°

(iv) 60°

Answer : (iii) 35°

21. In a ∆ABC, AB = AC. The value of x is ____.

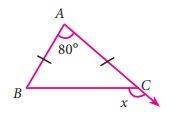
(i) 80°

(ii) 100°

(iii) 130°

(iv) 120°

Answer : (ii) 130°

22. If an exterior angle of a triangle is 115° and one of the interior opposite angles is 35°, then the other two angles of the triangle are

(i) 45°, 60°

 (ii) 65°, 80°

 (iii) 65°, 70°

 (iv) 115°, 60°

Answer : (ii) 65°, 80°

ANSWERS:

Exercise 4.1

1. yes

2. cannot draw a triangle

3. (i) 45º (ii) 62º (iii) 30º (iv) 17º (v) 18º (vi) 20º (vii) 24º (viii) 27º

4. ∠A = 60º; ∠B = 40º

5. 360º

6. 45º,60º,75º

7. 55º,60º,65º

8. 30º,60º,90º

9. ∠X = 60º; ∠Z = 48º

10. ∠A = 29º; ∠C = 61º

11. ∠M = 38º; ∠O = 52º

12.(i) 110º (ii) 11º

13. 21º

14. 110º

15. 120º

Objective type questions

16.(ii) 40º, 60º, 80º

17. (iii) 80º, 35º

18. (ii) 68º

19. (iii) x + y + z = 2(a + b + c)

20. (iii) 35º

21. (iii) 130º

22. (ii) 65º, 80º