Exercise 6.1 (Frequency Distribution Table, Graphical Representation)

Exercise 6.1

1. Fill in the blanks:

(i) Data has already been collected by some other person is _____________ data. [Answer: Secondary]

(ii) The upper limit of the class interval (25-35) is _____________. [Answer: 35]

(iii) The range of the data 200, 15, 20, 103, 3, 196, is _____________. [Answer: 197]

(iv) If a class size is 10 and range is 80 then the number of classes are _________. [Answer: 8]

(v) Pie chart is a __________ graph. [Answer: circular]

2. Say True or False:

(i) Inclusive series is a continuous series. [Answer: False]

(ii) Comparison of parts of a whole may be done by a pie chart. [Answer: True]

(iii) Media and business people use pie charts. [Answer: True]

(iv) A pie diagram is a circle broken down into component sectors. [Answer: True]

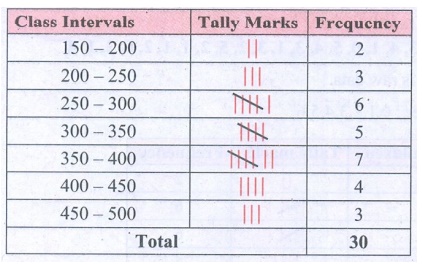
3. Represent the following data in ungrouped frequency table which gives the number of children in 25 families.

1,3,0,2,5,2,3,4,1,0,5,4,3,1,3,2,5,2,1,1,2,6,2,1,4

Solution:

The data given is raw data.

Ascending order : 0, 1, 2, 3, 4, 5, 6

∴ Tabulating in frequency distribution table we get

4. Form a continuous frequency distribution table for the marks obtained by 30 students in a X std public examination.

328, 470, 405, 375, 298, 326, 276, 362, 410, 255, 391, 370, 455, 229, 300, 183, 283, 366, 400, 495, 215, 157, 374, 306, 280, 409, 321, 269, 398, 200.

Solution:

Maximum mark obtained = 495

Minimum marks obtained = 157

Range = Maximum value − Minimum value

Range = 495 − 157

= 338

If we take the class size as 50 then the number of class intervals possible

= Range / Class size

= 338 / 50 = 6.76

≃ 7

5. A paint company asked a group of students about their favourite colours and made a pie chart of their findings. Use the information to answer the following questions.

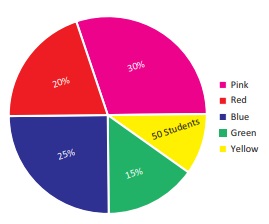
(i) What percentage of the students like red colour?

(ii) How many students liked green colour?

(iii) What fraction of the students liked blue?

(iv) How many students did not like red colour?

(v) How many students liked pink or blue?

(vi) How many students were asked about their favourite colours?

Solution:

Total percentage of students = 100%

∴ 50 students = 100% − (30% + 20% + 25% + 15%)

= 100% − 90%

50 students = 10%

10% of total students = 50

∴ 10/100 (total students) = 50

Total students = [ 50 × 100 ] / 10 = 500.

Total students = 500.

i) 20% of the students like red colour.

ii) 15% of the students liked green colour.

[ 15 / 100 ] × 500 = 75 students liked green colour.

iii) 25% students liked blue ⇒ 25/100 students liked blue.

=> 1/4 students liked blue.

iv) Percentage of students liked red colour = 20%

Percentage of students did not like red colour

= 100% − 20%

= 80%

∴  Number of students did not like red colour

= 80% of 500

= [ 80 / 100 ] × 500 = 400

400 students did not like red colour.

v) Students liked pink or blue = students liked pink + students liked blue.

= 30% of 500 + 25% of 500

= ( [30/100] × 500 ) + ( [25/100] × 500 )

= 150 + 125

= 275

vi) Total number of students = 500.

500 students were asked about their favourite colour.

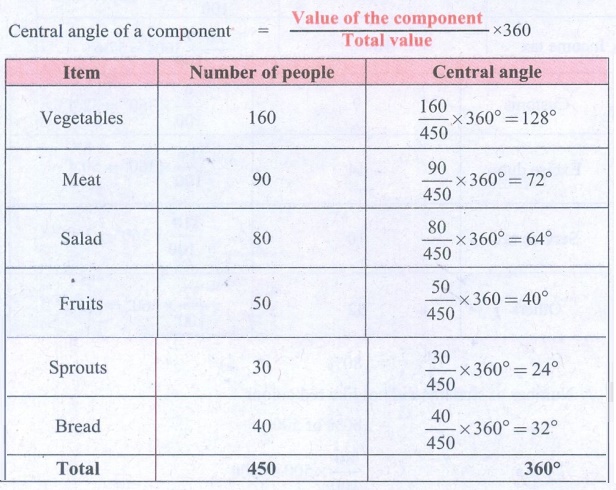
6. A survey gives the following information of food items preferred by people. Draw a Pie chart.

Solution:

Total number of people = 160 + 90 + 80 + 50 + 30 + 40 = 450

Converting the number of people prefer various food items into components part of 360°

Central angle of a component = [ Value of the component / Total value ] × 360

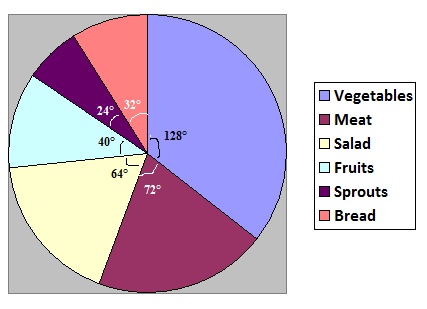
Food items preferred by people.

7. Income from various sources for Government of India from a rupee is given below. Draw a pie chart.

Solution:

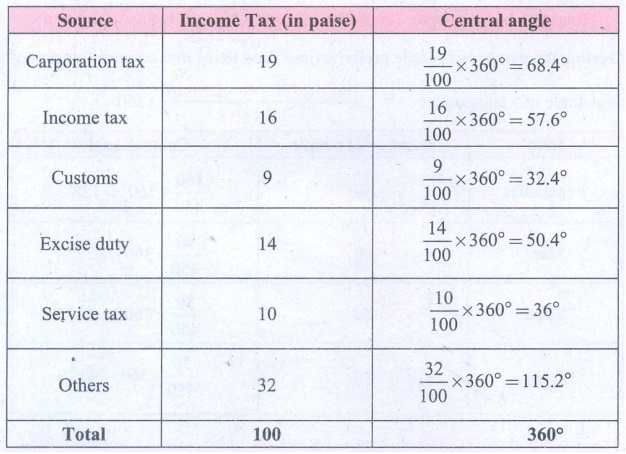
Income from various sources for Government of India in a rupee.

8. Monthly expenditure of Kumaran’s family is given below. Draw a suitable Pie chart.

Also

1. Find the amount spent for education if Kumaran spends ₹6000 for Rent.

2. What is the total salary of Kumaran?

3. How much did he spend more for food than education?

Solution:

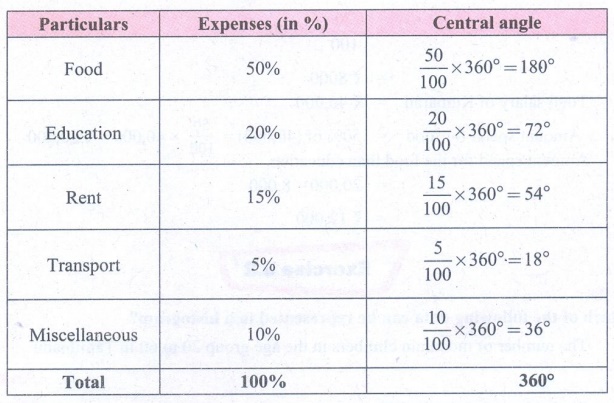
Monthly expenditure of Kumaran's family.

1. Given Kumaran spends ₹  6000 for Rent.

  ∴  15% of total expenditure = 6000

15/100 (Total Expenditure) = 6000

Total Expenditure = [6000 × 100] / 15

Total Expenditure = ₹ 40,000

Amount spend for education = 20% of total expenditure.

= [20 / 100] × 40,000

= ₹ 8000

2. Total salary of Kumaran = ₹ 40,000

3. Amount spend for food = 50% of (40,000) = [50/100] × 40,000 = ₹ 20,000

Amount spend for the food than education

= 20,000 − 8,000 =

= ₹ 12,000

Answer:

Exercise 6.1

1. (i) Secondary (ii) 35 (iii)197 (iv) 8 (v) Circular

2. (i) False (ii) True (iii) True (iv) True

5. (i) 20% (ii) 75 (iii) 1/4 (iv) 400 (v) 275 (vi) 500

8. (i) ₹8000 (ii) ₹40000 (iii) ₹12000