Chapter: Special Electrical Machines : Permanent Magnet Synchronous Motor
EMF Equation of BLPM Sine Wave Motor
EMF EQUATION OF BLPM SINE WAVE
MOTOR
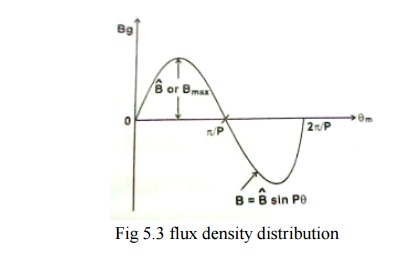
1. Flux density distribution
Flux
density can be expressed as B=||B|| sinθ or B
|cospθ or B sin(Pθ+a) or cos
(ρθ+α),2p=p,(i.e)p-no of pole pairs depending upon the position of the
reference axis as shown in fig6.3
Consider
a full pitched single turn armature coil as shown in fig 5.4.Let the rotor be
revolving with a uniform angular velocity of ὠm
mech.rad/sec.
At time t
= 0, let the axis of the single turn coil be along the polar axis.

2. EMF Equation of an ideal BLPM
sine wave motor
As per
faradays law of electromagnetic induction, emf induction in the single turn
coil.
e = -N d ɸ /dt

let the
armature winding be such that all turns of the phase are concentrated full
pitched and located with respect to pole axis in the same manner.
Let Tph
be the number of turns connected in series per phase. Then the algebraic
addition of the emfs of the individual turns gives the emf induced per phase as
all the emf are equal and in phase.


3. EMF equation of practical BLPM
sine wave motor
In a
practical BLPM sine wave motor at the time of design it is taken care to have
the flux density is sinusoidal distributed and rotor rotates with uniform
angular velocity. However armature winding consists of short chorded coils
properly distributed over a set of slot.
These
aspect reduce the magnitude of E ph of an ideal winding by a factor
Kw1 which is known as the winding factor the fundamental component
of flux.



Related Topics