Delay Estimation

DELAY ESTIMATION

Estimation of the delay of a Boolean function from its functional description is an important step towards design exploration at the register transfer level (RTL).

This addresses the problem of estimating the delay of certain optimal multi-level implementations of combinational circuits, given only their functional description.

The proposed delay model uses a new complexity measure called the delay measure to estimate the delay.

It has an advantage that it can be used to predict both, the minimum delay (associated with an optimum delay implementation) and the maximum delay (associated with an optimum area implementation) of a Boolean function without actually resorting to logic synthesisThe model is empirical and results demonstrating its feasibility and utility are presented.

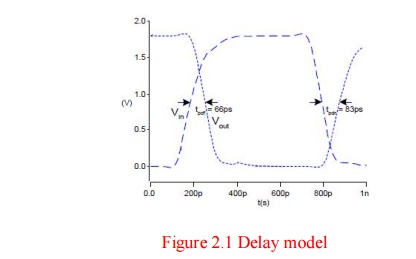
§   t_pdr: rising propagation delay

§   From input to rising output crossing V_DD/2

§   t_pdf: falling propagation delay

§   From input to falling output crossing V_DD/2

§   t_pd: average propagation delay tpd = (t_pdr + t_pdf)/2

§   t_r: rise time

§   From output crossing 20% to 80% V_DD

§   t_f: fall time

§   From output crossing 80% to 20% V_DD

§   t_cd: average contamination delay t_cd = (t_cdr + t_cdf)/2

§   t_cdr: rising contamination delay: Min from input to rising output crossing V_DD/2 t_cdf:

§   falling contamination delay: Min from input to falling output cross inV_DD/2

Solving differential equations by hand is hard. SPICE like simulators used for accurate analysis. But simulations are expensive. We need to be able to estimate delay although not as accurately as simulator.

§   Use RC delay models to estimate delay

§   C = total capacitance on the output node

§   Use Effective resistance R Therefore t_pd = RC

§   Transistors are characterized by finding their effective R.