Device and Circuit Characterization

DEVICE AND CIRCUIT CHARACTERIZATION

The modeling procedure is introduced in this chapter, taking into consideration the requirements for a good MOSFET analog model, discussed in the previous chapter. We note here two main aspects of our modeling approach;

a. The model must describe accurately all the operating regions in order to be integrated in a circuit simulator.

b. The current, conductance, and transconductance must be continuous in all regions of operation.

Our main goal in this chapter is to determine the drain current for any combination of terminal voltages. The chapter is divided into two main parts.

Throughout the first part, it is assumed that the channel is sufficiently long and wide, so that edge effects are confined to a negligible part of it.

While in the second part we incorporate the short and narrow channel effects to the model. We also assume that the substrate is uniformly doped.

The doping concentration will be assumed to be p-type and the modification to non uniform doping will be discussed later in this chapter.

1. Gradual Channel approximation (GCA)

Analytical or semi-analytical modeling of MOSFET characteristics is usually based on the so-called Gradual Channel Approximation (GCA).

In this approximation, we assume that the gradient of the electric field in the y direction, ∂F/∂y is much smaller than the gradient of the electric field in the x direction,∂F/∂x.

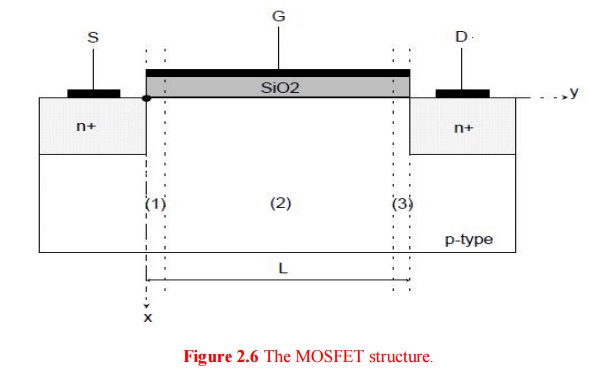
Which enable us to determine the inversion and depletion charge densities under the gate in terms of a one-dimensional electrostatic problem for the direction perpendicular to the channel? By applying of the two dimensional Poisson's equation for the semiconductor, refer to Fig. 2.1 region (2),

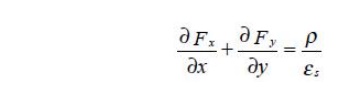
if we assume that the GCA is valid equation 2.2.1 may be approximated to the following one dimensional differential equation

we approach the source and drain junctions, the GCA becomes invalid (Fig. 2.11.1 regions (1) and (3)) because of the increasing longitudinal field due to the pn junctions which make ∂F/∂y comparable or even larger than ∂F/∂x .

However, for the long channel MOSFET's these transition regions can be neglected with respect to the total length of the device. In order to account for the effect of these regions, it is necessary to use two dimensional analysis requiring a numerical solution.

2. Validity of the GCA

The validity of GCA can be checked by making rough estimates of the variation in the longitudinal and vertical field components. We will establish expressions that allow the GCA to be checked under strong inversion.

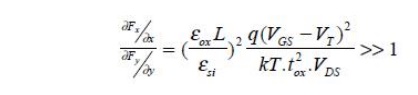
3. The long channel current model

The derivation of the dc drain current relationship recognizes that, in general, the current in the channel of a MOSFET can be caused by both drift and diffusion current. In an NMOSFET we may assume the following resonableapproximation :

i- The drain current is mainly carried by electrons .

ii- The current flows almost in the y direction.

iii- No sources or sinks in the channel.

Note that in weak inversion the surface potential along the channel in long channel MOSFETs is almost constant. Thus ∂Fy/∂y is very small, implying that ∂Fy/∂y<<∂Fx/∂x.

T hus in long channel MOSFET the GCA is valid both in strong and weak inversion regions . Which enable us to reach to the following general relationship of drain current.

4. General Drift-Diffusion current equation in MOSFET:

This is the drift-diffusion drain current of the form

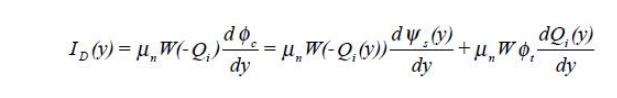
where μn is the electron surface mobility in the channel, W is the channel width, Qi is the inversion charge density per unit area, φc is the quasi Fermi potential (the difference between Efn at the surface of the semiconductor a d Efp in the bulk of the semiconductor), ψs is the surface potential referenced to the bulk potential, and φt is the thermal voltage (=kT/q).

The first term is the drift current component, while the second term is the diffusion current component. In both components, μn is the electrons' surface mobility being less than the mobility in the bulk due to surface scattering.

5. Voltage-Charge equation from the Transverse electric field:

In order to eliminate the electron charge density Qi term in the current charge equation, a second relationship is required that relates the electron charge density to the applied potentials.

Using the relationship between voltage and charge appearing across the MOS capacitor we have

Cox (VG -φ ms -ψ s )= -(Qi+QB+Qox+Qit )

where VG is the gate voltage referenced to the bulk potential, φms is the metal semiconductor work function difference, QB is the depletion (bulk impurity) charge density per unit area, Qox is the sum of the effective net oxide charge per unit area at the Si-SiO2 interface, and Qit is the interface trapped charge density per unit area.

Different approximations have been introduced in order to express the different MOS charges (QB, Qox, Qit) in terms of the applied voltages, then using eq. to compute the inversion charge density Qi.

The resulting charge is then used in eq.to determine the drain current; Four main approaches then follow, after them we shall discuss the proposed approach recently developed in ICL1 and modified by this work.