Electric potential: Definition of Electric potential and Relation between electric field and potential

Electric potential

Let a charge +q be placed at a E points, in the electric field. When a unit  Electric potential positive charge is moved from A to B against the electric force, work is done. This work is the potential difference between these two points. i.e., dV = WA ->' B.

The potential difference between two points in an electric field is defined as the amount of work done in moving a unit positive charge from one point to the other against the electric force.

The unit of potential difference is volt. The potential difference between two points is 1 volt if 1 joule of work is done in moving 1 Coulomb of charge from one point to another against the electric force.

The electric potential in an electric field at a point is defined as the amount of work done in moving a unit positive charge from infinity to that point against the electric forces.

Relation between electric field and potential

Let the small distance between A and B be dx. Work done in moving a unit positive charge from A to B is dV = E.dx.

The work has to be done against the force of repulsion in moving a unit positive charge towards the charge +q. Hence,

dV = -E.dx

E = -dV/dx

The change of potential with distance is known as potential gradient, hence the electric field is equal to the negative gradient of potential.

The negative sign indicates that the potential decreases in the direction of electric field. The unit of electric intensity can also be expressed as Vm-1.

1. Electric potential at a point due to a point charge

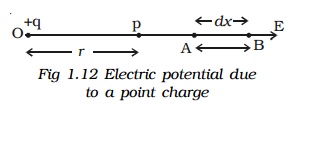
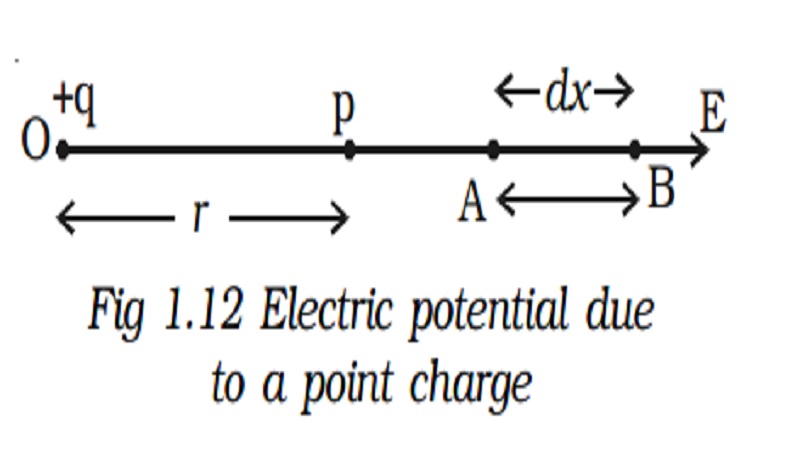
Let +q be an isolated point charge situated in air at O. P is a point at a distance r from +q. Consider two points A and B at distances x and x + dx from the point O (Fig.1.12).

The potential difference between A and B is,

dV = -E dx

The force experienced by a unit positive charge placed at A is

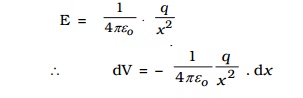
The negative sign indicates that the work is done against the electric force.

The electric potential at the point P due to the charge +q is the total work done in moving a unit positive charge from infinity to that point.

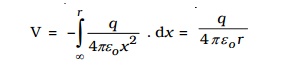
2. Electric potential at a point due to an electric dipole

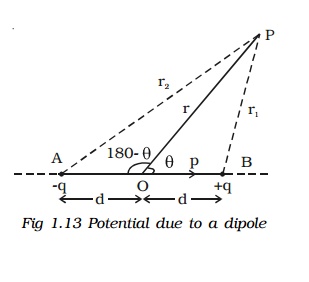
Two charges xq at A and +q at B separated by a small distance 2d constitute an electric dipole and its dipole moment is p (Fig 1.13).

Let P be the point at a distance r from the midpoint of the dipole O and ? be the angle between PO and the axis of the dipole OB. Let r1 and r2 be the distances of the point P from +q and xq charges respectively.

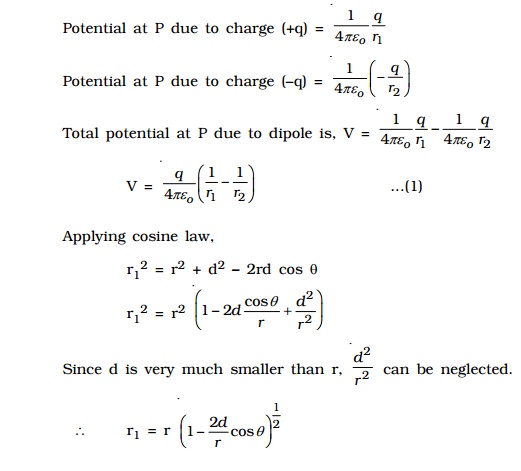
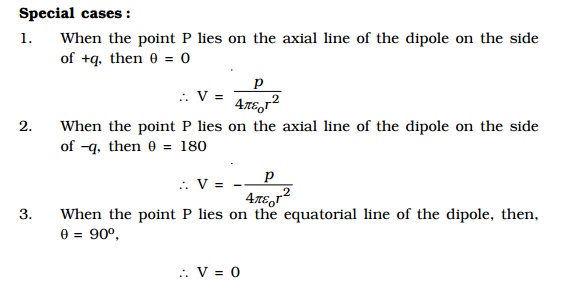
3. Electric potential Energy

The electric potential energy of two point charges is equal to the work done to assemble the charges or workdone in bringing each charge or work done in bringing a charge from infinite distance.

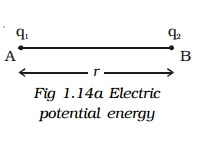
Let us consider a point charge q1, placed at A (Fig 1.14a].

The potential at a point B at a distance r from the charge q1 is

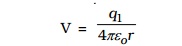
Another point charge q2 is brought from infinity to the point B.

Now the work done on the charge q2 is stored as electrostatic potential energy (U) in the system of charges q1 and q2.

Keeping q2 at B, if the charge q1 is imagined to be brought from infinity to the point A, the same amount of work is done.

Also, if both the charges q1 and q2 are brought from infinity, to points A and B respectively, separated by a distance r, then potential energy of the system is the same as the previous cases.

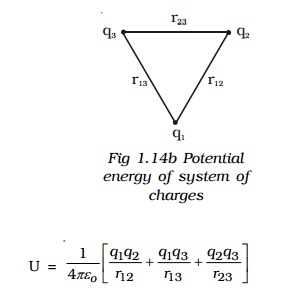
For a system containing more than two charges (Fig 1.14b), the potential energy (U) is given by

4. Equipotential Surface

If all the points of a surface are at the same electric potential, then the surface is called an equipotential surface.

(i) In case of an isolated point charge, all points equidistant from the charge are at same potential. Thus, equipotential surfaces in this

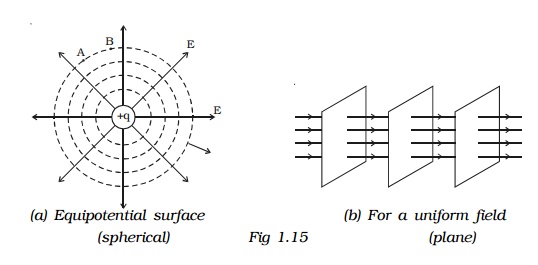
case will be a series of concentric spheres with the point charge as their centre (Fig 1.15a). The potential, will however be different for different spheres.

If the charge is to be moved between any two points on an equipotential surface through any path, the work done is zero. This is because the potential difference between two points A and B is defined as VB - VA = WAB/q . If VA = VB then WAB = 0. Hence the electric field lines must be normal to an equipotential surface.

(ii) In case of uniform field, equipotential surfaces are the parallel planes with their surfaces perpendicular to the lines of force as shown in Fig 1.15b.